Linear Track
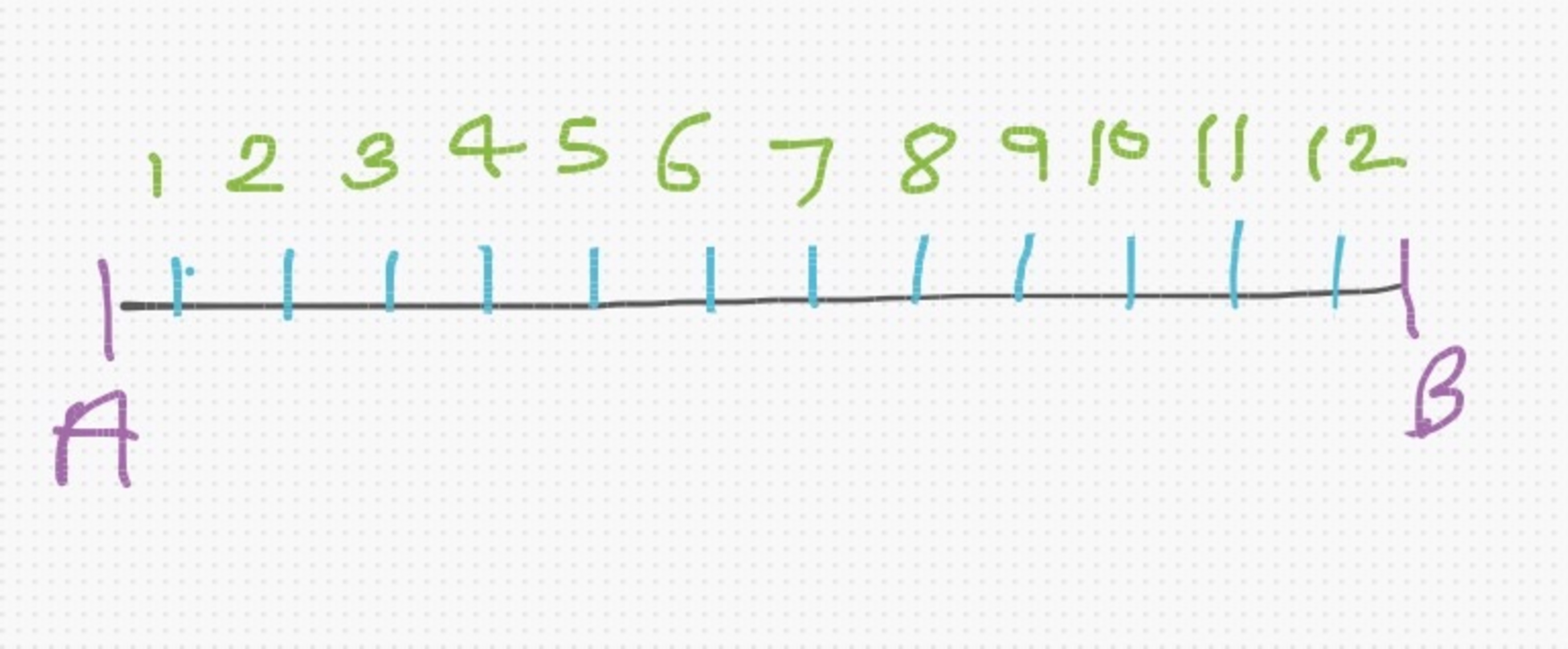
There are 12 Stations in a row as shown in the figure. A train stops at 4 stations such that no stops are at consecutive stations.How many such selections are possible?
The answer is 126.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Moderator note:
For clarity, you should avoid reusing notation. The stations were already numbered with 1 to 12, and using "non-stopping stations are marked as 1, 2, ... 8" might give others the wrong impression.
Initially, let's remove the 4 stopping stations
Then we are left with 8 non-stopping stations (=12-4) as shown below
. 1 . 2 . 3 . 4 . 5 . 6 . 7 . 8 .
(non-stopping stations are marked as 1,2 ... 8)
Now there are 9 positions (as marked by . ) to place the 4 stopping stations
such that no two stopping stations are consecutive
This can be done in 9C4 ways
Hence, required number of ways = 9C4 =126