Again Not the Deathly Hallows Symbol
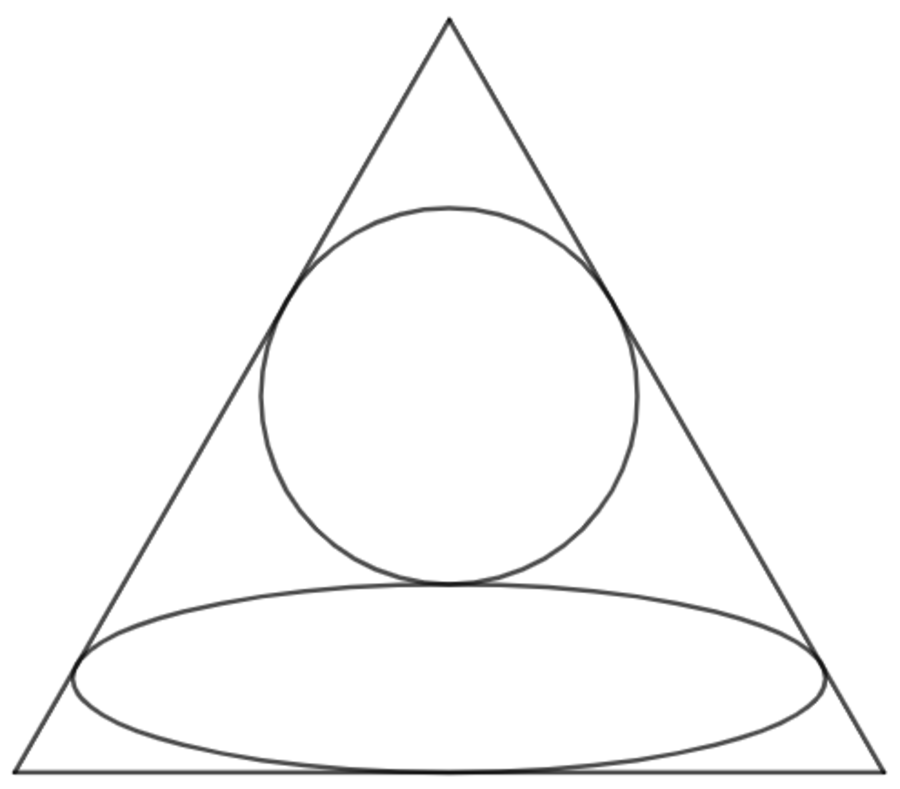
As shown above, one ellipse and one circle are arranged in an equilateral triangle. There exists the unique value of eccentricity such that:
- The horizontally-positioned ellipse whose major axis is parallel to one of the three legs shares three points of tangency with the triangle and one point of tangency with the circle.
- The circle tangent to the triangle at two points has the same area as the ellipse.
Input as your answer.
The answer is 968245.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If the radius of the circle is r and the semimajor and semiminor axes of the ellipse are a , b , then r 2 = a b and the ellipse
a 2 x 2 + b 2 ( y − b ) 2 = 1 must be tangent to the two lines y = 3 r + 2 b ± x 3 , and hence 3 a 2 + b 2 3 a 2 a 2 = ( 3 r + b ) 2 = 9 r 2 + 6 r b = 3 a b + 2 b a b so that ( 1 − 3 u ) 2 = 4 u 3 where u = a b . Thus we deduce that u = 4 1 (the other solution u = 1 may be a solution of this last equation, but the corresponding b = a is not a solution of the previous equation - squaring an equation can create bogus solutions). Thus the eccentricity is e = 1 − u 2 = 4 1 1 5 , which makes the answer 9 6 8 2 4 5 .