AIME Problem 4
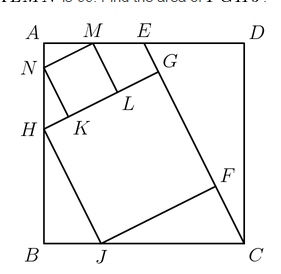 In the diagram below,
A
B
C
D
is a square. Point
E
is the midpoint of
A
D
. Points
F
and
G
lie on
C
E
, and
H
and
J
lie on
A
B
and
B
C
, respectively, so that
F
G
H
J
is a square. Points
K
and
L
lie on
G
H
, and
M
and
N
lie on
A
D
and
A
B
, respectively, so that
K
L
M
N
is a square. The area of
K
L
M
N
is 99. Find the area of
F
G
H
J
.
In the diagram below,
A
B
C
D
is a square. Point
E
is the midpoint of
A
D
. Points
F
and
G
lie on
C
E
, and
H
and
J
lie on
A
B
and
B
C
, respectively, so that
F
G
H
J
is a square. Points
K
and
L
lie on
G
H
, and
M
and
N
lie on
A
D
and
A
B
, respectively, so that
K
L
M
N
is a square. The area of
K
L
M
N
is 99. Find the area of
F
G
H
J
.
This problem is part of this set .
The answer is 539.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
A l l △ s h a v e s i d e s i n r a t i o o f 1 : 2 : 5 . L e t A B = B C = p , B J = n , A M = m . ∴ H J = 5 n . . . . . ( 1 ) J G = J C ∗ 5 2 = ( p − n ) ∗ 5 2 . . . ( 2 ) ( 1 ) = ( 2 ) , 5 n = ( p − n ) ∗ 5 2 , ∴ n = 7 2 p . . . ( 3 ) ∴ H B = 2 n = 7 4 p . . . . ( 4 ) A l s o N M = 5 m . . . . . . . . . ( 5 ) U s i n g ( 4 ) , N K = N H ∗ 5 2 = ( A B − A N − H B ) ∗ 5 2 = ( p − m − 7 4 p ) ∗ 5 2 = ( 7 3 p − m ) ∗ 5 2 . . . . ( 6 ) ( 5 ) = ( 6 ) , 5 m = ( ( 7 3 p − m ) ∗ 5 2 , ∴ m = 7 2 6 p . . . ( 7 ) F r o m ( 3 ) a n d ( 7 ) A r e a F G H J = 5 ∗ 4 9 2 ( 6 p ) 2 5 ∗ 7 2 ( 2 p ) 2 ∗ 9 9 = 5 3 9 You method is better. I have given above just little different method. We can use analytical geometry also.
Nice and simple
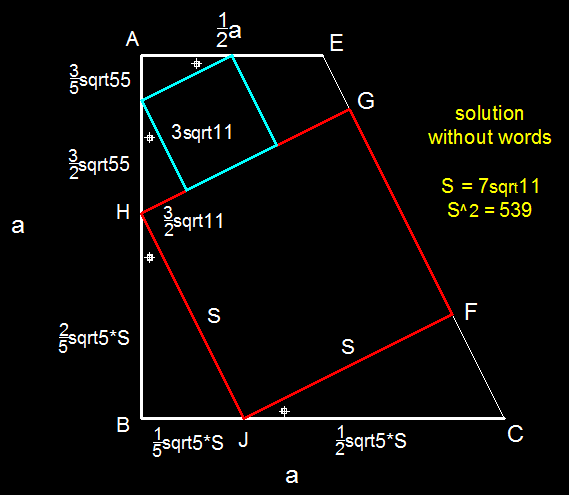
We note that △ C D E ≡ △ J F C ≡ △ H B J ≡ △ N K H ≡ △ M A N are similar triangles with side lengths in the ratio of 1 : 2 : 5 .
Now, let the side lengths of square A B C D , K L M N and F G H J be a , b = 9 9 = 3 1 1 and x respectively. Then, we have:
a = A B = A N + N H + H B = 5 1 b + 2 5 b + 5 2 x
a = B C = B J + J C = 5 1 x + 2 5 x
Equating the two equations, we have:
5 1 b + 2 5 b + 5 2 x 5 1 x + 2 5 x − 5 2 x 2 5 x − 5 1 x ( 2 5 5 − 2 ) x 3 x ⇒ x = 5 1 x + 2 5 x = 5 1 b + 2 5 b = 5 1 b + 2 5 b = ( 2 5 2 + 5 ) b = 7 b = 7 1 1
The area of square F G H J = x 2 = 4 9 × 1 1 = 5 3 9