AIMO 2015 Q6

Geometry Level 4

A large circle with radius 30 / π 30/ \sqrt{\pi} is shaded grey. Two white circles with diameter 30 / π 30/ \sqrt{\pi} lie inside the grey circle such that they are all tangent to one another (the two circles are internally tangent to the grey circle but are externally tangent to each other). Two more white circles of equal radii lie inside the grey circle such that both small white circles are internally tangent to the grey circle and are externally tangent to both white circles but are not tangent to each other. Find the area of the grey portion visible.


The answer is 250.

View wiki
Sharky Kesa by Sharky Kesa , 19, United Kingdom

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Let the radius of the small white circle be r r . Then we have:

( 15 π + r ) 2 − ( 15 π ) 2 + r = 30 π ( 15 π + r ) 2 − ( 15 π ) 2 = 30 π − r ( 15 π + r ) 2 − ( 15 π ) 2 = ( 30 π − r ) 2 ( 15 π ) 2 + 2 r ( 15 π ) + r 2 − ( 15 π ) 2 = 4 ( 15 π ) 2 − 4 r ( 15 π ) + r 2 6 r ( 15 π ) = 4 ( 15 π ) 2 ⇒ r = 4 6 ( 15 π ) = 10 π \begin{aligned} \sqrt{\left(\frac{15}{\sqrt{\pi}}+r \right)^2 - \left(\frac{15}{\sqrt{\pi}} \right)^2} + r & = \frac{30}{\sqrt{\pi}} \\ \sqrt{\left(\frac{15}{\sqrt{\pi}}+r \right)^2 - \left(\frac{15}{\sqrt{\pi}} \right)^2} & = \frac{30}{\sqrt{\pi}} - r \\ \left(\frac{15}{\sqrt{\pi}}+r \right)^2 - \left(\frac{15}{\sqrt{\pi}} \right)^2 & = \left(\frac{30}{\sqrt{\pi}} - r\right)^2 \\ \left(\frac{15}{\sqrt{\pi}} \right)^2 + 2r\left(\frac{15}{\sqrt{\pi}} \right) +r^2 - \left(\frac{15}{\sqrt{\pi}} \right)^2 & = 4 \left(\frac{15}{\sqrt{\pi}} \right)^2 - 4r\left(\frac{15}{\sqrt{\pi}} \right) +r^2 \\ 6r\left(\frac{15}{\sqrt{\pi}} \right) & = 4 \left(\frac{15}{\sqrt{\pi}} \right)^2 \\ \Rightarrow r & = \frac{4}{6} \left(\frac{15}{\sqrt{\pi}} \right) \\ & = \frac{10}{\sqrt{\pi}} \end{aligned}

The area of the grey portion visible:

A = π ( 30 π ) 2 − 2 π ( 15 π ) 2 − 2 π ( 10 π ) 2 = 3 0 2 − 2 ( 1 5 2 ) − 2 ( 1 0 2 ) = 900 − 450 − 200 = 250 \begin{aligned} A & = \pi \left(\frac{30}{\sqrt{\pi}} \right)^2 - 2 \pi \left(\frac{15}{\sqrt{\pi}} \right)^2 - 2 \pi \left(\frac{10}{\sqrt{\pi}} \right)^2 \\ & = 30^2-2(15^2) - 2(10^2) \\ & = 900 - 450 - 200 \\ & = \boxed{250} \end{aligned}

9 Helpful 0 Interesting 0 Brilliant 0 Confused

I did it basically the same way, just in general and substituted 15/√π for R (the radius of the bigger white circle, got r=2/3R and 10/9πR^2 for the grey area visible) in the end.

It is very easy to reconstruct my solution from Chew-Seong Cheong's, simply by replacing 15/√π by R and 30/√π by 2R.

(The first equation comes from calculating the altitude of the isosceles triangle (by using Pythagoras' theorem) formed by the two black line segments and the segment of the "horizontal" diameter of the grey circle. The sum of the altitude of the triangle and r equals to the ("vertical" on the picture) radius of the grey circle (2R).)

Zee Ell - 5 years, 6 months ago

Log in to reply

And mine was the same as Zee Ell, I find it better to write a small letter than the value every time.

A Former Brilliant Member - 5 years, 6 months ago

How do you construct the image?

Jai Jain - 5 years, 6 months ago

Log in to reply

I used Excel spreadsheet and paint. It took me quite a while.

Chew-Seong Cheong - 5 years, 6 months ago

Yes Exactly Same Way Sir!

Kushagra Sahni - 5 years, 6 months ago

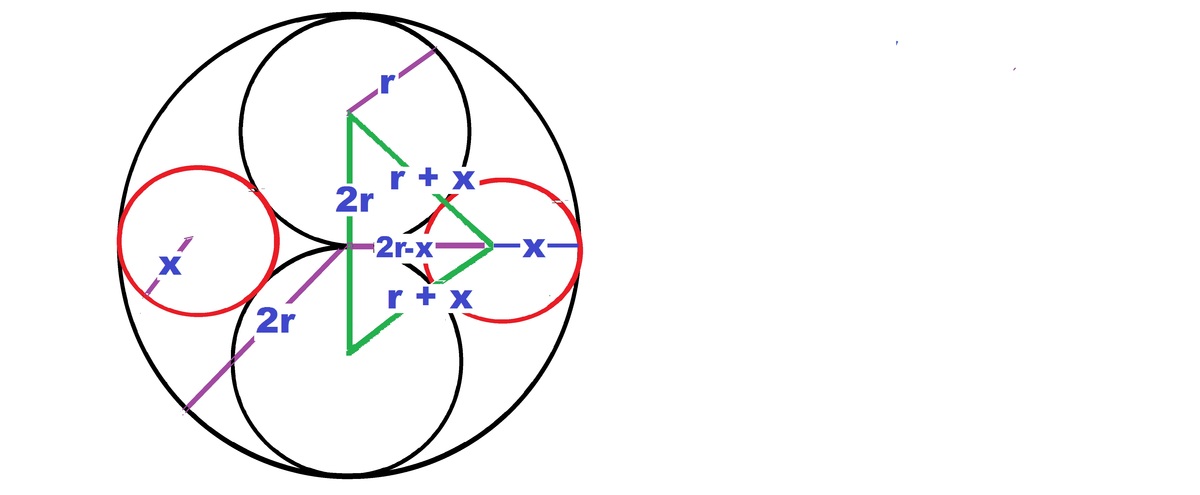
Let the radius of the gray circle be 2r, and that of small white x. The centers of big white circles and right small one form an isosceles triangle with base as two big white circle center =2r. Small and big circle centers are (r+x) apart. The altitude on the base is (2r - x). But the altitude of this triangle is also = ( r + x ) 2 − ( 2 r / 2 ) 2 = ( 2 r − x ) 2 . ⟹ 6 x r = 4 r 2 . r ≠ 0 , ∴ x = 2 3 r . ∴ g r a y a r e a = π { ( 2 r ) 2 − 2 ∗ r 2 − 2 ∗ ( 2 3 r ) 2 } = π ∗ 10 9 ∗ r 2 . B u t 4 r = 30 π . ∴ r = 15 2 ∗ π . ∴ g r a y a r e a = 250 (r+x)^2 - (2r/2)^2 =(2r-x)^2. ~~ \implies ~ 6xr=4r^2. ~ r\neq0, ~\therefore ~ x=\dfrac 2 3 r.\\ \therefore ~ gray ~ area ~ =\pi\{ (2r)^2 - 2*r^2 - 2*(\dfrac 2 3 r)^2\}=\pi*\dfrac {10} 9 *r^2.\\ But ~~ 4r=\dfrac {30}{\sqrt \pi} . ~ \therefore ~r= \dfrac {15}{2*\sqrt \pi}.\\ \therefore ~ gray ~ area =\Large ~~~~~\color{#D61F06}{250}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...