Air resistance

Classical Mechanics Level 2

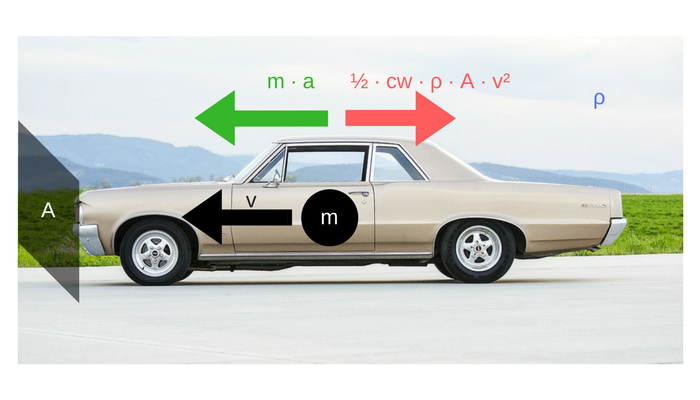
On a free highway, a car accelerates uniformly with constant acceleration $a = 1 \, \frac{\text{m}}{\text{s}^2}$ . Taking into account the air resistance, the equation of motion for the velocity $v$ reads

$m \cdot \frac{d v}{dt} = m \cdot a - \frac{1}{2} \cdot c_w \cdot \rho \cdot A \cdot v^2$

with the mass $m = 800 \,\text{kg}$ and cross-sectional area $A = 2 \text{m}^2$ of the car and the density $\rho = 1.25 \frac{\text{kg}}{\text{m}^3}$ of the air. The dimensionless factor $c_w$ describes the drag coefficient, that depend on the actual shape of the car.

After a few minutes of acceleration the car reaches its top speed of $v_\infty = \lim_{t \to \infty} v(t) = 144 \, \frac{\text{m}}{\text{s}}$ . What is the value of the drag coefficient $c_w$ ?

Bonus question: What is the actual solution for the differential equation?

0.4 0.67 1 0.15 1.33

1 solution

Markus Michelmann
Sep 11, 2017

In the limiting case $t \to \infty$ the velocity approches a constant value $v_\infty$ , so that the total accelation $\frac{dv}{dt}$ becomes zero. The equation of motion can be simplified to

$0 = m a - \frac{1}{2} c_w \rho A v_\infty^2 \qquad \Rightarrow \qquad c_w = \frac{2 m a}{\rho A v_\infty^2} = \frac{2 \cdot 800 \cdot 1}{1.25 \cdot 2 \cdot 1600} = 0.4$

It seems we have two different values for the limiting velocity. 144 in the problem, and 40 in the solution.

Steven Chase - 3 years, 9 months ago

The velocity in the problem should reads 144 km/h = 40 m/s. Thanks for your comment, I have corrected the units.

Markus Michelmann - 3 years, 9 months ago

Air resistance

1 solution

0 pending reports