Airborne -Approach Speed (Revision 2)
Inspiration: Airborne Biker, by Shane Sarosh
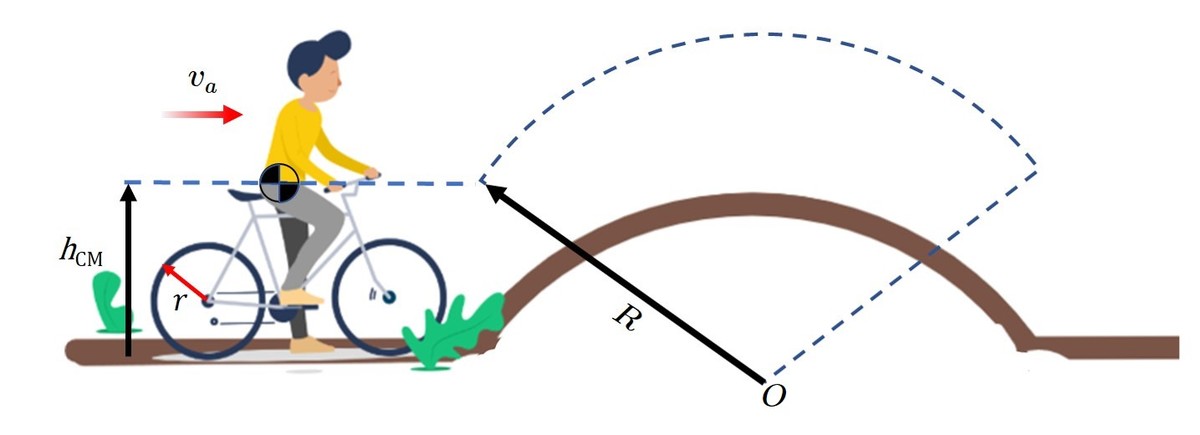
When approaching a jump, the rider gets up to speed, levels the pedals, and slightly bends the knees to prepare for take off!
Assumptions:
-
( Vertical distance of Rider+ Bike Center of Mass )
-
( Radius the CoM follows until liftoff )
-
( Outside radius of bicycle wheel/tire)
-
( Mass Moment of Inertia of a single wheel )
-
( Mass of Rider + Bike )
-
-
No Drag or Frictional Losses
-
rolling without slipping
What is the minimum approach speed in such that the the rider becomes airborne at the top of the hump?
Round answer to the nearest 10th.
The answer is 7.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Performing a force balance at the onset of liftoff the contact normal force tends to zero, and the net force acting on the body is the weight:
∑ F v = m g = m R v 2 ⇕ = g R
To determine the minimum speed required on the flat to achieve the liftoff speed we can use Conservation of Energy:
K E + P E = K E ′ + P E ′
On the LHS ( The Approach Energy ) we have Translational + Rotational (wheels) energy ( taking this to be the datum for potential energy ):
2 1 M v a 2 + I ω a 2 = 2 1 M v a 2 + r 2 I v a 2 = β v a 2
Where;
β = 2 1 M + r 2 I
On the RHS ( The Liftoff Energy ) we have Translational + Rotational ( wheels ) + Potential energy. Looking at each in turn:
Translational
2 1 M v 2
Rotational ( wheels )
I ω 2 = r 2 I v 2
Potential:
m g ( R − h C M )
Finally, solving for v a
β v a 2 = m g ( R − h C M ) + β v 2
v a = β m g ( R − h C M ) + v 2
v a ≈ 7 . 5 s m
As always, If I've bungled this analysis ( and problem ) please speak up. It usually takes me several revisions to get things in order.