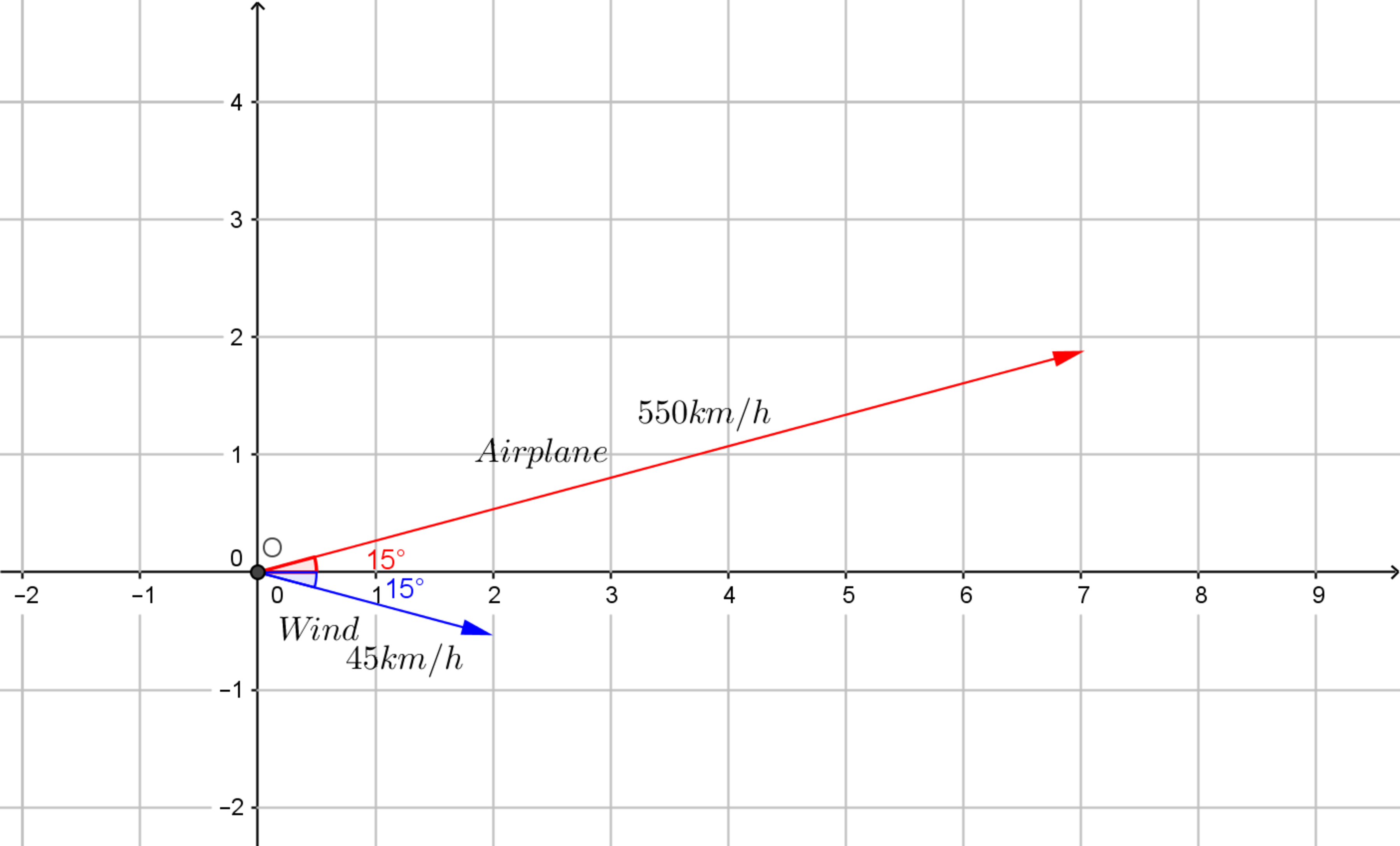
Airplanes and their confusing paths!

Geometry Level pending

An airplane is flying in the direction 15 $^\circ$ North of East at 550 km/h. A wind is blowing in the direction 15 $^\circ$ South of East at 45 km/h. Find the actual speed ("ground speed") of the airplane in integer. ( Hint : Don't forget the wind!)

563 km/h 595 km/h 577 km/h 589 km/h

1 solution

Marta Reece
Apr 30, 2017

In one hour, the plane will move from point $A$ to point $B$ .

The angle between the direction $AC$ and $CB$ is $15^\circ+15^\circ=30^\circ$ , so within the $\triangle ABC$ the $\angle ACB=150^\circ.$

Law of cosines applied to $\triangle ABC$ provides the distance $x=\sqrt{550^2+45^2-2\times550\times45\times\cos150^\circ}=5\sqrt{990\sqrt{3}+12181}\approx\boxed{589}$

Airplanes and their confusing paths!

1 solution

0 pending reports