Two-Digit Puzzle

$Let\quad the\quad 2\quad digit\quad number\quad be\quad 10x+y\quad where\quad x>y\\ We\quad know\quad 8(x+y)\quad +\quad 1\quad =\quad 10x+y\quad \quad \quad \quad \quad and\\ \quad \quad \quad \quad \quad \quad 13(x-y)\quad +\quad 2\quad =\quad 10x+y\\ \\ Solving\quad the\quad system\quad of\quad linear\quad equations\quad in\quad 2\quad variables,\\ we\quad get:\quad \boxed { x=4 } \quad and\quad \boxed { y=1 }$ $Thus\quad the\quad number\quad is\quad 41.$

Also notice:

Let x be our 2-digit number. x must be one more than a multiple of 8, i.e. x =8 a +1 for some integer a . Going through the different 2-digit possibilities for x , (17, 25, 33, 41, 49, 57, 65, 73, 81, 89, 97), 41 is the only possibility where a happens to be the sum of the digits of x .

Likewise, we are given x must be two more than a multiple of 13, i.e. x =3 b +2 for some integer b . Going through the different 2-digit possibilities for x , (15, 28, 41, 54, 67, 80, 93), 41 is the only possibility where b happens to be the difference of the digits of x .

You really only need one of the premises in order to solve the problem. Additionally, 41 is the only number that is on both lists, so the fact that we are dealing with sums and differences of digits is irrelevant if given both premises.

The second condition is redundant. Let $10a+b$ be our 2-digit number.

The first condition gives: $10a+b=8(a+b)$

$a=\frac{1}{2}(7b+1)$ . Since $a,b$ are digits between 0 and 9, we can only have $b=1,a=4$

let t=tens digit

and u=units digit

so the the two digit #=10t + u

10t + u=8(t+u)+1

10t + u=13(t-u)+2

t=4 and u=1

therefore the # is 41

Let the first digit be $X$ and the second digit be $Y$

From the first condition we have that $10X + Y = 1 + 8(X+Y) \implies 2X - 7Y = 1$

From the second condition we have that $10X + Y = 2 + 13|X-Y|$

From the first equation, $2X - 7Y = 1 \implies 2X = 7Y + 1 \implies 2X > 7Y \implies X > \frac{7}{2}Y \implies X > Y$

Combining the previous fact with the second equation,

$10X + Y = 2 + 13|X-Y| \implies 10X + Y = 2 + 13(X-Y) \implies 3X - 14Y = -2$

We now have the following system of equations

$\begin{cases} 2X - 7Y = 1\\ 3X - 14Y = -2 \end{cases}$

Solving it yield: $X = 4, Y = 1$ Therefore, the number is $41$

N = 10p + q = 8(p + q) + 1 = 13|p - q| + 2
2p = 7q + 1 < 20
7q < 20 - 1 = 19
q < 19/7 ==> 0 ≤ q < 3
2p = 7q + 1
LHS is even, so RHS should also be even.
Then, 7q must be odd. ==> q must be odd, too.

The only odd number in the above range is q = 1, thus p = 4
N = 10 x 4 + 1 = 41

I used code to solve this and dont mind the first three lines of output:

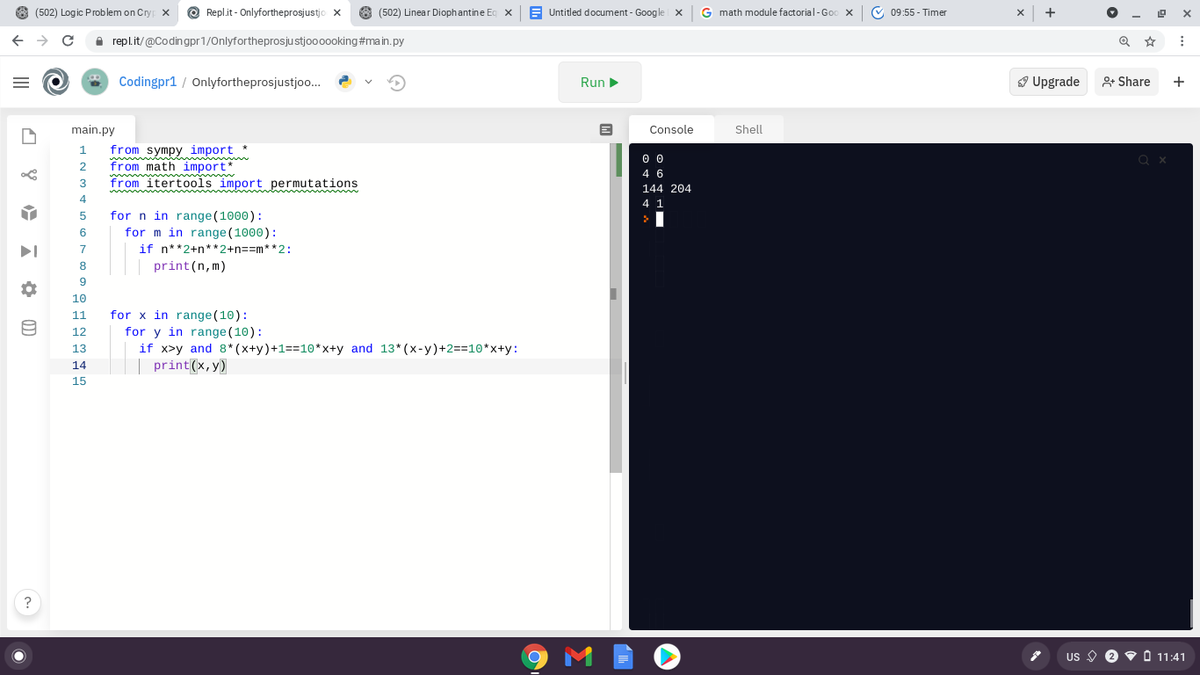
From the second part the answer must be 2 modulo 13, but from the first part it must be 1 modulo 8 (in particular it must be odd) That only allows for 15, 41, 67, 93 of which only 41 is 1 modulo 8..