Alex's inscribed circle
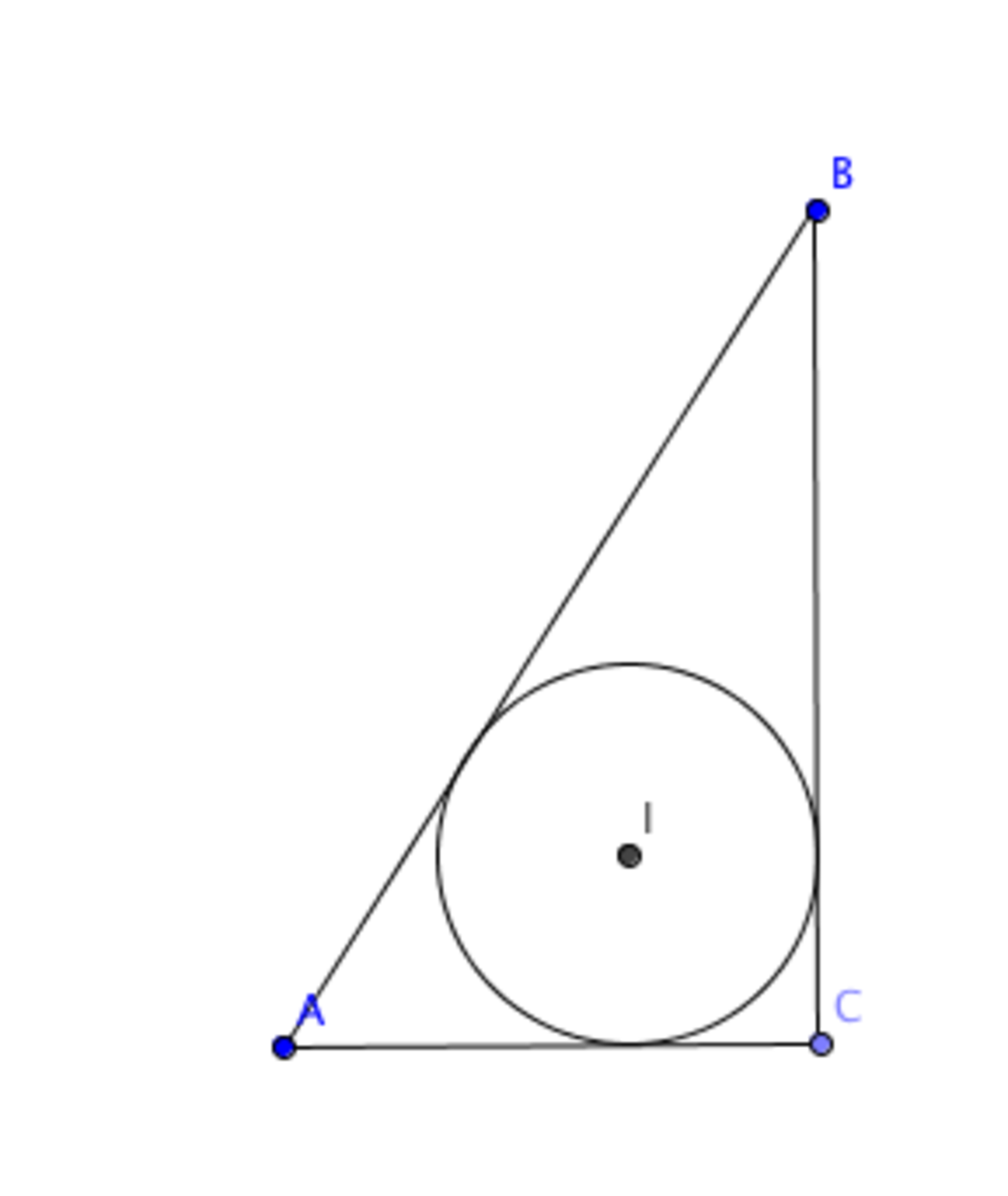
Right triangle △ A B C has side lengths A B = 5 1 , A C = 2 4 , and C B = 4 5 . If the area of the inscribed circle of △ A B C can be written as a π , what the value of a ?
This problem is posed by Alex R.
The answer is 81.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
21 solutions
Let X , Y , and Z be the points of tangency of the circle to the triangle sides A B , B C , and C A , respectively. By the ice-cream cone theorem (a special case of a Power of a Point), A X = A Z , B X = B Y , and C Y = C X . Thus we have three unknowns for the lengths of the perimeter of the triangle, and three equations, namely A X + B X = 5 1 , B Y + C Y = 4 5 , and A Z + C Z = 2 4 .
After solving, we are especially interested in C Y = C Z = 9 . Since we know ∠ I Y C = ∠ I Z C = ∠ Y C Z = 9 0 ∘ and C Y = C Z , I Y C Z is a square. Thus the radius of the circle is I Y = Y C = 9 . The area is 8 1 π , so our answer is 8 1 .
We know the radius of a circle inscribed inside a right triangle can be found from
Radius = (45+24-51)/2 =9
Therefore the area of the circle is (pi)(9^2)
Therefore a=81
We know that, the radius r of the circle inscribed in a right triangle can be defined as,
r = 2 a + b − c
where, c is the hypotenuse and a and b are the other two sides.
Putting in the values of A B , A C and C B in the identity, we get,
r = 2 4 5 + 2 4 − 5 1 = 2 1 8 = 9
So, the area of the circle is,
π r 2 = π × 9 2 = 8 1 π
Hence, the value of a is 8 1 .
inradius=area/semi perimeter=(1/2 * 45 *24)/(45+24+51)/2=540/60=9,so area of circle=pi * 9^2=81pi
radius= triangular area/k = √k(k-a)(k-b)(k-c) / k where k=1/2(a+b+c) where a, b and c are the side lengths of the triangle a= 51 b=24 c=45
k= 1/2(51+24+45) k= 1/2(120) k=60
radius= √60(60-51)(60-24)(60-45) / 60 radius=√60(9)(36)(15) / 60 radius=√291600 / 60 radius=540/60 radius=9
area=r^2 π area=9^2 π area=81 π therefore a=81
En español:
Siendo un circulo inscrito en un triángulo el radio del circulo sera igual al inradio. Teniendo la formula del área de un triangulo
A
=
s
r
Donde:
A es el area, s el semiperimetro y r el inradio.
Despejando \(r ) \( r=A/s \)
El área es igual a A = ( B a s e ∗ A l t u r a ) / 2 = ( 2 4 ∗ 4 5 ) / 2 = 5 4 0 . El semiperimetro es igual a s = ( A B + A C + C B ) / 2 = ( 5 1 + 2 4 + 4 5 ) / 2 = 6 0 .
Reemplazando r = A / s = 5 4 0 / 6 0 = 9 Como el área del circulo es igual a r 2 ∗ π el resultado es 9 2 = 8 1
Using the relation, in-radius, r = s Δ where Δ is the are of the triangle and s the semi-perimeter. Hence r = 9 . So, the answer is 8 1 .
Let point of contact be D,E and F on AC,CB and BA respectively. Let CD=CE=x, since tangent drawn from a point to a circle are of equal length then BE=BF=45-x, therefore again using above theorem we have, AF=AD=6+x , since AF+FB=AB=51, this implies (6+x)+x=24 (i.e. AD+DC=AC) so, x=9, which is the radius of circle area=9 9 pi so a=81
r = area of triangle/semi-perimeter As area of in-circle = aπ, r = √a = (0.5 24 45)/{0.5(24+45+51)} = (24*45)/120 = 9 or a = 81
Let us draw perpendiculars from point I on sides AB, BC, CA. Let's call the feet of these perpendiculars as points D,E,F respectively. Now let the radius of the circle be r. therefore, ID = IE = IF = FC = CE = r Also BE=(45-r) and AF=(24-r) By properties of congruence of two triangles, we can easily show that the triangles IFA and IDA are congruent, so are the triangles IEB and IDB. Hence, EB = DB = (45-r) and AF = AD = (24-r) but AB = AD + DB so 51 = (45-r) + (24-r) Solving this we get r = 9 and area of circle = 81 pi
You can find the radius of the inscribed circle of a triangle by formula r=L/s. L=(24x45)/2=540 and s=(24+45+51)/2=60 and we get r=540/60=9. The area of the circle can be ound by formula L=r^2xpi and a=r^2=81
Note 24^2 + 45^ 2= 51^2, therefore ABC is a right triangle, and therefore its circumradius is equal to half the hypotenuse, or 51/ 2.
Using equation r = a b c/ 4 s R, where r is the triangle's in radius, a,b,c its sides, and s its semi perimeter, so r=9, therefore the inscribed circle's area is equal to 81π, and a=81.
We see that the incircle formula gives inradius=(45+24-51)/2=9
Let the intersection of circle centred at I with △ A B C , 's sides AB, BC , CA be D,E,F Since , A D = A F , B D = B E , C F = C E . & radius of circle r = C F ( since, C B ⊥ A C ) , s = semi perimeter of triangle .
Since , s = ( A B + B C + A C ) / 2 = A D + B E + C F . = A B + r ( A D + B E = A D + B D )
We have ( 5 1 + 2 4 + 4 5 ) / 2 = 5 1 + r . ,
r = 9 .
So , area of circle = π ∗ r 2 = 8 1 ∗ r
a*pi is the area of triangle
a=r^2
x=51; y=24; z=45; s=(x+y+z)/2 R=(s (s-x) (s-y)*(s-z))^(1/2)/s
a=(s (s-x) (s-y)*(s-z))/s^2
a=60 9 36 15/60 60=81
Let r=radius;
r=(BC+CA-AB)/2 r=(45+24-51)/2 r=9
The area of the circle is 81π. Therefore a=81.
Moderator note:
You should be careful and explain the conditions for which your equation r = ( B C + C A − A B ) / 2 holds
First, we must find the radius r, from the equation of the area of the triangle ABC: (24 r)/2 + (45 r)/2 + (51 r)/2 = (24)(45)/2. We get r = 9. Then the Area is aπ = 81 π. So a = 81.
Note 2 4 2 + 4 5 2 = 5 1 2 , therefore A B C is a right triangle, and therefore its circumradius is equal to half the hypotenuse, or 2 5 1 . Through the equation r = 4 s R a b c , where r is the triangle's inradius, a , b , c its sides, and s its semiperimeter, we obtain r = 9 , therefore the inscribed circle's area is equal to 8 1 π , and a = 8 1 .
we know that tangent lines in a certain intersection point have the same length. and by using ratios, we can get the length of the three pair of tangent lines: 9, 15,36..
the area of a circle is π r 2 the radius of the circle is the tangent line with a right angle, in this case, 9 so the area is π 9 2 = 81 π and a = 81
Moderator note:
Great approach, realizing that in a right triangle, the radius has length equal to one of the tangents.
The semiperimeter of the triangle is 60, and as the area is 2 4 ⋅ 4 5 , the radius of the inscribed triangle is 6 0 2 4 ⋅ 4 5 = 9 . As the radius is 9, the area is 8 1 π .
r = (area of triangle)/(semiperimeter) = 9. Hence are of circle =81*(p1) , so a=81