Is it a telescopic series?

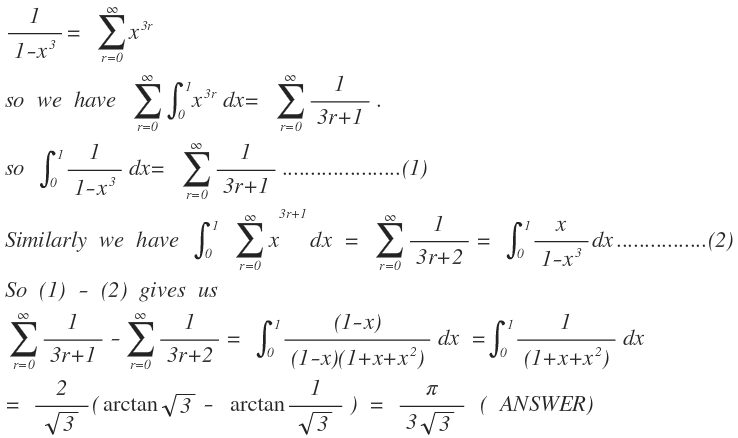
Question is easy if you know the concept of interchanging summations and integrals.First we write the required sum as :

$S=\displaystyle \sum _{ r=0 }^{ \infty }{ \frac { 1 }{ (3r+1)(3r+2) } }$

We know that :

$\large \int _{ 0 }^{ x }{ { y }^{ 3r }dy } =\frac { { x }^{ 3r+1 } }{ 3r+1 }$

Integrating it again with respect to $x$ and putting limits $0$ to $1$ we get :

$\large \int _{ 0 }^{ 1 }{ \int _{ 0 }^{ x }{ { y }^{ 3r }dy } dx } =\int _{ 0 }^{ 1 }{ \frac { { x }^{ 3r+1 } }{ 3r+1 } dx } =\frac { 1 }{ (3r+1)(3r+2) }$

So in the expression of S we replace our general term with our integration expression to get :

$\large S=\displaystyle \sum _{ r=0 }^{ \infty }{ \int _{ 0 }^{ 1 }{ \int _{ 0 }^{ x }{ { y }^{ 3r }dy } dx } }$

Here comes the main trick what we do now is interchange integral and the summation to get :

$\large S=\int _{ 0 }^{ 1 }{ \int _{ 0 }^{ x }{\displaystyle \sum _{ r=1 }^{ \infty }{ { y }^{ 3r } } dy } dx }$

After interchanging we see that our summation has now become an infinite G.P. hence applying the formula for infinte G.P we get :

$\large S=\int _{ 0 }^{ 1 }{ \int _{ 0 }^{ x }{ \frac { 1 }{ 1-{ y }^{ 3 } } dy } dx }$

Now the thing left is a not so simple double integral which can be evaluated with good amount of hard work and it comes out to be :

$\large \boxed{S=\frac { \pi }{ 3\sqrt { 3 } }}$

$\begin{aligned} L & = \sum_{r=0}^\infty \left(\frac 1{3r+1} - \frac 1{3r+2} \right) \\ & = 1 - \frac{1}{2} + \frac{1}{4} - \frac{1}{5} + \frac{1}{7} - \frac{1}{8} + ... \end{aligned}$

Now consider the Maclaurin series of $-\ln (1-z)$ , where $z$ is a complex number:

$\begin{aligned} -\ln(1-z) & = z + \frac{z^2}{2} + \frac{z^3}{3} + \frac{z^4}{4} + \frac{z^5}{5} + \frac{z^6}{6} + ... \quad \quad \small \color{#3D99F6}{\text{Let }z = e^{\frac{2\pi}{3}i}} \\ -\ln(1-e^{\frac{2\pi}{3}i}) & = e^{\frac{2\pi}{3}i} + \frac{e^{\frac{4\pi}{3}i}}{2} + \frac{e^{2\pi i}}{3} + \frac{e^{\frac{8\pi}{3}i}}{4} + \frac{e^{\frac{10\pi}{3}i}}{5} + \frac{e^{4\pi i}}{6} + ... \quad \quad \small \color{#3D99F6}{\text{Taking the imaginary part both sides}} \\ \Im \left[-\ln(1-e^{\frac{2\pi}{3}i})\right] & = \sin \frac{2\pi}{3} + \frac{\sin \frac{4\pi}{3}}{2} + \frac{\sin 2\pi}{3} + \frac{\sin \frac{8\pi}{3}}{4} + \frac{\sin \frac{10\pi}{3}}{5} + \frac{\sin 4\pi}{6} + ... \quad \quad \small \color{#3D99F6}{\text{Note that } -1 < \sin \frac{2k\pi}{3} < 1} \\ \Im \left[-\ln \left(1+ \frac{1}{2} - \frac{\sqrt{3}}{2}i \right)\right] & = \frac{\sqrt{3}}{2} - \frac{\sqrt{3}}{2} \cdot \frac{1}{2} + \frac{0}{3} + \frac{\sqrt{3}}{2} \cdot \frac{1}{4} - \frac{\sqrt{3}}{2} \cdot \frac{1}{5} + \frac{0}{6} + ... \\ \Im \left[-\ln \left(\frac{3}{2} - \frac{\sqrt{3}}{2}i \right)\right] & = \frac{\sqrt{3}}{2}\left( 1 - \frac{1}{2} + \frac{1}{4} - \frac{1}{5} + \frac{1}{7} - \frac{1}{8} + ... \right) \\ \Im \left[-\ln \left(\sqrt{3}\left(\frac{\sqrt{3}}{2} - \frac{1}{2}i \right) \right)\right] & = \frac{\sqrt{3}}{2} \cdot L \\ \implies L & = \frac{2}{\sqrt{3}} \cdot \Im \left[-\ln \left(\sqrt{3} e^{-\frac{\pi}{6}i} \right)\right] \\ & = \frac{2}{\sqrt{3}} \cdot \Im \left[-\ln \sqrt{3} + \frac{\pi}{6}i \right] \\ & = \frac{\pi}{3\sqrt{3}} \approx \boxed{0.605} \end{aligned}$

Any one here used a python code? :D

Got 0.604598676967

The easiest way is to mention few terms: $\frac{1}{1}$ - $\frac{1}{2}$ + $\frac{1}{4}$ - $\frac{1}{5}$ + $\frac{1}{7}$ - $\frac{1}{8}$ ...etc. We notice, we are summing over (0,1) the following integral $\int$ $\frac{1-x}{1-x^3}$ = $\frac{\pi}{3\sqrt{3}}$

http://scipp.ucsc.edu/~haber/ph116A/powertheorems.pdf