My first problem

We can use Newton's sums method to solve this problem. Let $P_n = a^n + b^n + c^n$ , $S_1 = a+b+c =P_1=0$ , $S_2 = ab+bc+ca$ and $S_3 = abc$ . Then, we have:

\(\begin{array} {} P_2 = a^2+b^2+c^2 = S_1P_1 -2S_2 = 0 - 2S_2 & = -2S_2 \\ P_3 = a^3+b^3+c^3 = S_1P_2 -S_2P_1 + 3S_3 = 0 - 0 + 3S_3 & = 3S_3 \\ P_4 = a^4+b^4+c^4 = S_1P_3 -S_2P_2 + S_3P_1 = 0 - S_2(-2S_2) + 0 & = 2S_2^2 \\ P_5 = a^5+b^5+c^5 = S_1P_4 -S_2P_3 + S_3P_2 = 0 - S_2(3S_3) + S_3(-2S_2) & = -5S_2S_3 \end{array} \)

$\Rightarrow \dfrac{(a^3+b^3+c^3)^2(a^4+b^4+c^4)}{(a^5+b^5+ c^5)} = \dfrac{P_3^2P_4}{P_5^2} = \dfrac{(3S_3)^2(2S_2^2)}{(-5S_2S_3)^2} = \dfrac{18}{25}$

$\Rightarrow m + n = 18 + 25 = \boxed{43}$

The problem allows substituting any three non-zero real values for a , b and c as long as $a+b+c=0$ and the denominator is non-zero.

Let $a=2$ and $b=c=-1$ .

Substituting gives:

$\dfrac{ (8-1-1)^2 \cdot (16+1+1) }{ (32-1-1)^2 } =$

$\dfrac{ 6^2 \cdot 18 }{ 30^2 } = \dfrac{ 18 }{ 5^2 } = \dfrac{ 18 }{ 25 } = \dfrac{ m }{ n }$

So $m + n = 18 + 25 = 43$ .

By the statement we have a+b+c=0. Then, we have :

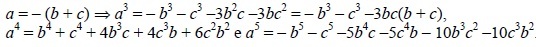
replacing the expression

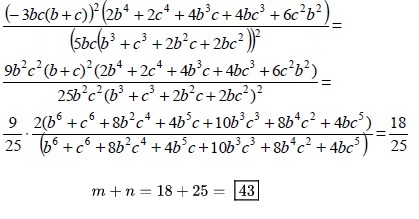
I used Newton sum here.

First finding $(a^3+b^3+c^3)$ .

$a^3+b^3+c^3=(a+b+c)(a^2+b^2+c^2)-(ab-bc-ca)(a+b+c)+3abc$
$a^3+b^3+c^3=3abc$
$\Rightarrow (a^3+b^3+c^3)^2=\boxed{9(abc)^2}$

Second finding $(a^4+b^4+c^4)$ .

$a^4+b^4+c^4=(a^2+b^2+c^2)^2-2[(ab)^2+(bc)^2+(ca)^2]$
$a^4+b^4+c^4=[(a+b+c)^2-2(ab+bc+ca)]-2[(ab)^2+(bc)^2+(ca)^2]$
$\Rightarrow a^4+b^4+c^4=\boxed{2[(ab)^2+(bc)^2+(ca)^2]}$

Third finding $(a^5+b^5+c^5)$ .

$a^5+b^5+c^5=(a+b+c)(a^4+b^4+c^4)-(ab+bc+ca)(a^3+b^3+c^3)+abc(a^2+b^2+c^2)$
$a^5+b^5+c^5=(ab+bc+ca)(-5abc)$
$\Rightarrow (a^5+b^5+c^5)^2=(ab+bc+ca)^2(-5abc)^2=\boxed{[(ab)^2+(bc)^2+(ca)^2](-5abc)^2}$

$\Rightarrow \dfrac{(a^3+b^3+c^3)^2(a^4+b^4+c^4)}{(a^5+b^5+c^5)^2}$

$\Rightarrow \dfrac{9(abc)^2×2[(ab)^2+(bc)^2+(ca)^2]}{[(ab)^2+(bc)^2+(ca)^2]×25(abc)^2}$

$\Rightarrow \dfrac{18}{25}=\dfrac{m}{n}$

$\Rightarrow m+n=18+25=\boxed{43}$