Algebra needed?
As shown in the figure above,
A
B
D
is a straight line; the triangle
A
B
C
is similar to the triangle
B
D
E
. Given that
B
F
:
F
C
=
D
G
:
G
E
=
3
:
1
, the area of the triangle
A
B
C
is 24. Find the area of the shaded region (triangle
A
F
G
).
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
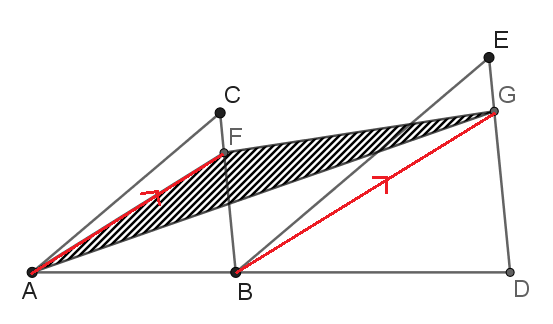 Connect
B
G
. It is clear that
A
F
∥
B
G
. Then the area of triangle
A
F
G
is same as the area of the triangle
A
F
B
, which is
4
3
×
2
4
=
1
8
.
Connect
B
G
. It is clear that
A
F
∥
B
G
. Then the area of triangle
A
F
G
is same as the area of the triangle
A
F
B
, which is
4
3
×
2
4
=
1
8
.
If we assume, as the question implies, that the area of △ A F G is the same for any measurements such that △ A B C is similar to △ B D E , B F : F C = D G : G E = 3 : 1 , and the area of △ A B C = 2 4 , then we can solve it for an easy specific case that satisfies those conditions, for example, △ A B C ≅ △ B D E , ∠ A B C = ∠ B D E = 9 0 ° , A B = B D = 1 2 , B C = D E = 4 , B F = D G = 3 , and F C = G E = 1 .

Then △ A F G has a base F G = B D = 1 2 and a height of F B = 3 , for an area of A = 2 1 b h = 2 1 ⋅ 1 2 ⋅ 3 = 1 8 .