Perfect train. Perfect speed. Perfect Tunnel.

It takes 1 hour for the back of the train to reach the tunnel, and 1 hour for it to go through the tunnel.

Relevant wiki: 1D Kinematics Problem Solving

Given that,

• Tunnel length = 10 km

• Speed of the train = 10 km/h

The time will take for the front and back of train to get through the tunnel= 1 hour.

The time will take for the back of the train to reach the tunnel = 1 hour

So the entire train will take $1 + 1 = \boxed{2}$ hours to get through the tunnel,

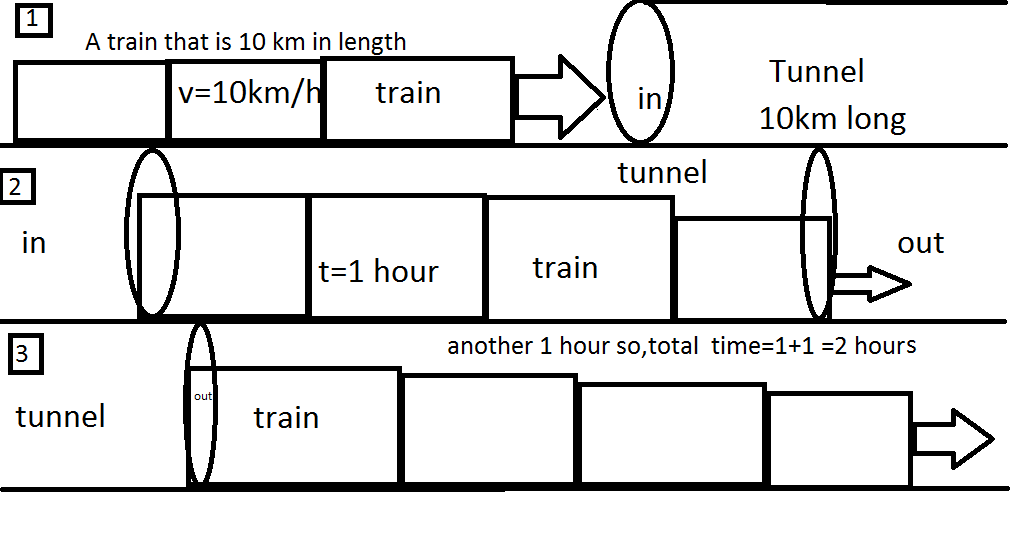
It says A train that is $10$ km in length traveling at $10$ km/hour is about to enter a tunnel that is $10$ km long. because the tunnel is $10$ km long the train speeds is $10$ km per hour means the velocity of it is $10$ km in $1$ hour, so,

After $1$ hour we will see its head( the front of the train ) on the exit point of the tunnel but the tail of that train (the back of the train) will remain on the entry point. So It will take another $1$ hour to see its tail on the exit point. So It will take $2$ hours to see the train totally out of that tunnel .

if the train exits the tunnel, then it has to pass through the tunnel with its whole body.

so, after passing 10 km, the exit pole will be seen,but the whole train is still under the tunnel.so,the train has to move another 10 km to remove its body from the tunnel.

now, total path= $10+10=20$ km, the train goes 10 km in 1 hour.so, it will take 2 hours to exist the tunnel fully.

$V=speed; d=distance; t=time$

$t=\dfrac{d}{V}$

$d=\text{length of the train plus length of the tunnel}=10+10=20~km$

Substituting, we get

$t=\dfrac{20}{10}=2~hours$

T=D/S, T=(10+10)/10=2

Step 1. The train is 10km long therefore it takes one hour to get to the end of the tunnel. Step 2. For the train to fully exit it needs another hour because it is 10km long. Time taken: 2 hours

start from the distance between the back of the train and the end of the tunnel (20km), so as the train moves at the same speed at the front and the back, how long does it take to run 20km at 10km/h?... thats 20/10=2

I think the most simplest solution is to make the train a simple near lengthless line perpendicular to the track(lengthless horizontally) by pulling it back from its nose to the end part. Now this simple object has to travel a distance of- 10+10=20. Now using same old equations in physics we get t= 2hrs.

The front will exit in one hour; the back end enters at the same time and exits one hour later. 1+1=2

It takes the train 1 hour to get through the tunnel but the question is asking for the entire train to get through the tunnel hence the answer is 2 hours

v=d/t t=2hrs