Sequential roots
a , b and c are positive real numbers satisfying a + b + c = 1 0 0 . The maximum value of
a + a b + 3 a b c
can be expressed as n m , where m and n are coprime positive integers. What is the value of m + n ?
The answer is 403.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Great solution!
I was wondering if there is way to solve it using Cauchy-Schwarz inequality. From AM-GM,
a + a b + 3 a b c ≤ 6 1 1 a + 5 b + 2 c .
From Cauchy-Schwarz,
( 1 1 a + 5 b + 2 c ) 2 ≤ ( a 2 + b 2 + c 2 ) ( 1 5 0 ) .
Is there a way to proceed from this step?
Any help is appreciated. Thanks!
Log in to reply
i can't proceed with it as sum of a, b, c is constant and Not sum of their squares. Even otherwise, your first equality occurs for a:b:c = 1:1:1 and second one for 11:5:2....so i wonder how to solve even if sum of squares of a, b, c were given constant..?? Again, admire help..gratitude in advance. :)
Log in to reply
In fact the only way I can see to relate a 2 + b 2 + c 2 to a + b + c is to use QM-AM but that gives us the bound in the wrong direction :-/ hopefully someone can perhaps shed some light on this :)
How did you know that you need to take 2 a + 4 b while taking AM-GM. Should we take 2 a + b
Log in to reply
Kumar, nice question :) Maybe you would like to see my solution for the motivation of these "strange" coefficients?
What if a=b=c=100/3 ? Then the value would be even smaller.
what is that a+4b/2 from? why not a+b/2
i read all 4 solutions but no one actually mention the part which leads to a=4b=16c, it's quite hard to solve though.
Since this is an inequality question and there are square (and cube) roots in the question, one natural method to use is AM-GM .
My first instinct was to use AM-GM directly on the roots: a + a b + 3 a b c ≤ a + 2 a + b + 3 a + b + c . This means that I want to minimize b and c . However, they cannot be 0 since then the product would be 0 and the expression is minimized, instead of maximized and so we are stuck.
Conclusion: we cannot just use AM-GM directly.
Next, I tried something else:
By AM-GM, we have a b ≤ 2 a + b , which is equivalent to 2 a b ≤ a + b and similarly 3 3 a b c ≤ a + b + c . With this in mind, we try to write a b and 3 a b c in the given expression as 2 x a × y b and 3 3 k a × m b × n c , respectively (where x × y = 4 and k × m × n = 2 7 ), so that from AM-GM we have that a + 2 x a × y b + 3 3 k a × m b × n c ≤ a + x a + y b + k a + m b + n c .
The reason we do this is because we are given the value of a + b + c , so if we can choose values of x , y , k , m , n such that the RHS is a multiple of a + b + c , then we can find a maximum for the given expression. Then we need the coefficients of a , b , c to be equal to each other: in other words, 1 + x 1 + k 1 = y 1 + m 1 = n 1 .
Given that x × y = 4 and k × m × n = 2 7 , to make life easier, we can set x = 4 and y = 1 so that 1 = 1 / y , which changes the equation to 4 1 + k 1 = m 1 = n 1 − 1 .
To help, in order for the maximum to even be achievable, both of the AM-GM inequalities need to hold, meaning that x a = y b and k a = m b = n c . But this means that y x = b a = m k , so we need to have m k = 1 4 = 4 , or k = 4 m . Then since we also need 4 1 + k 1 = m 1 , we can see that 4 1 = 4 m 3 , or m = 3 . Then this gives k = 1 2 and n = 3 4 .
Hence we have (due to AM - GM): a + 2 4 a × b + 3 3 1 2 a × 3 b × 3 4 c ≤ a + 4 a + 1 2 a + 3 b + 3 4 c = 3 4 × ( a + b + c ) , with equality achieved when 4 a = b and 1 2 a = 3 b = 3 4 c , which happens when a = 2 1 1 6 0 , b = 2 1 4 0 and c = 2 1 1 0 .
Putting this into the context of the question, we get the maximum is n m = 3 4 × ( a + b + c ) = 3 4 × 1 0 0 = 3 4 0 0 . Hence, m + n = 4 0 3 .
Although this can be greatly simplified, I think it is better to share my thoughts and motivations.
Great explanation of your first instinct. I knew that was what most people would attempt too, and get stuck. Glad to see that you can push through, and even provide a reasonable explanation for the choice of 'strange' coefficients used lated.
I agree that it was wise of you to share your thoughts and motivations, and I see that several other people agree too. Keep it up!
Log in to reply
agree...thanks
Sir it took 10-11 minutes to solve this question and maximum 25 minutes for your high level questions but I don't know why I usually see median time to solve tough questions over 45-200 minutes!
I can't seem to get why Anqi arbitrarily set x = 4 and y = 1 . We have a system of 5 equations and 5 variables, so did she just get lucky and guess the solution correctly?
I'm sorry I meant set y = 1
And I also forgot to mention that equality holds when a = 4 b = 1 6 c :P
Thanks, great writeup. It seems the key point is that we want to make an AM-GM where (a+b+c) appears on the AM side , as opposed to trying to substitute out one of the variables.
Hey, somewhere half the way in the solution, I think you switched the signs. It should've been a + 2 a / x × b / y + 3 3 a / k × b / m × c / n ≤ a + a / x + b / y + a / k + b / m + c / n . That is, ≤ and not ≥
Also, in the line where you mention k = 1 2 , m = 3 , n = 4 / 3 , the value of n over there must be 3 / 4 .
One more thing: The ratio should've been k : m : n = 1 6 : 4 : 1
But on the whole, SIMPLY AWESOME EXPLANATION!
I always search for this kind of solution, i very appreciate you for sharing your motivation!!
Excellent one..beautiful
long solution
Lemma
Let a , b , c be the positive real numbers . Then a + a b + 3 a b c ≤ 3 4 ( a + b + c ) holds . Equality when a = 4 b = 1 6 c
Proof
a + a b + 3 a b c = a + 2 4 a . b + 3 3 1 2 a . 3 b . 3 4 c Using AM-GM inequality , a + 2 4 a . b + 3 3 1 2 a . 3 b . 3 4 c ≤ a + 4 a + b + 1 2 a + 3 b + 3 4 c Which is equal to 3 4 ( a + b + c ) . which completes the proof of lemma .. inequality holds when 1 2 a = 3 b = 3 4 c ⟹ a = 4 b = 1 6 c □ .
So using the lemma , we have
a + a b + 3 a b c ≤ 3 4 ( 1 0 0 ) = 3 4 0 0 So maximum value is 3 4 0 0 Thus m + n = 4 0 3 □
Awesome..
Let a + b + c = S . Note that by AM-GM inequality,
a b ≤ 2 2 1 a + 2 b
3 a b c ≤ 3 4 1 a + b + 4 c
Combining these, we have a + a b + 3 a b c ≤ 3 4 S . Further, we can verify that equality occurs at ( a , b , c ) = ( 2 1 1 6 S , 2 1 4 S , 2 1 1 S ) . Hence, the answer is 3 4 S = 3 4 0 0 .
By using Cauchy inequality, we have:
2 a + 2 b ≥ 2 a b
4 a + b + 4 c ≥ 3 3 a b c .
Therefore, a + a b + 3 a b c ≤ 3 4 ( a + b + c ) .
Therefore, a + a b + 3 a b c max = 3 4 0 0 when 4 a = b = 4 c = 2 1 4 0 0 .
The answer is: 400+3=403.
it's AM-GM not Cauchy
Log in to reply
The AM-GM inequality is attributed to Cauchy.
Log in to reply
This may be a debatable fine point. Cauchy certainly provided a proof of the AM-GM inequality. Primacy of discovery is not always clear for mathematical theorems. I jokingly say, "In mathematics, theorems are named after their most recent discoverer."
This solution was possible only after help from Sreejato Bhattacharya. Since a , b , c are positive reals, we have
2 a + 4 b ≥ 2 a b ⟹ 4 a + 4 b ≥ a b
Again, 3 a + 4 b + 1 6 c ≥ 4 3 a b c ⟹ 1 2 a + 4 b + 1 6 c ≥ 3 a b c
Adding, we get,
4 a + 4 b + 1 2 a + 4 b + 1 6 c ≥ a b + 3 a b c
Simplification of L.H.S leads to
1 2 4 a + 1 6 b + 1 6 c ≥ a b + 3 a b c . Adding a to both sides
a + 1 2 4 a + 1 6 b + 1 6 c ≥ a + a b + 3 a b c
⟹ 1 2 1 6 ( a + b + c ) ≥ a + a b + 3 a b c
Thus, a + a b + 3 a b c ≤ 3 4 × 1 0 0 = 3 4 0 0
You also have to show that equality occurs.
What level would you say these problems are at? Close to national math olympiads, or higher than this
equality occurs when a = 4 b = 1 6 c . The values can easily be computed using a + b + c = 1 0 0 .
Applying the AM-GM inequality, we have:
a + a b + 3 a b c
= a + 2 1 a . 4 b + 4 1 3 a . 4 b . 1 6 c
≤ a + 4 a + 4 b + 1 2 a + 4 b + 1 6 c
= 3 4 ( a + b + c ) = 3 4 0 0
The equality occurs iff a = 2 1 1 6 0 0 , b = 2 1 4 0 0 , c = 2 1 1 0 0
So m + n = 4 0 3
Let x = a / 1 6 , y = b / 4 , and z = c , so a = 1 6 x , b = 4 y , and c = z . Then the given condition a + b + c = 1 0 0 becomes 1 6 x + 4 y + z = 1 0 0 . We want to maximize $$a + \sqrt{ab} + \sqrt[3]{abc} = 16x + 8 \sqrt{xy} + 4 \sqrt[3]{xyz}.$$
By the AM-GM inequality, x y ≤ ( x + y ) / 2 and 3 x y z ≤ ( x + y + z ) / 3 , so
1 6 x + 8 x y + 4 3 x y z ≤ 1 6 x + 4 ( x + y ) + 3 4 ( x + y + z ) = 3 4 ( 1 6 x + 4 y + z ) = 3 4 0 0 .
Equality occurs when x = y = z = 1 0 0 / 2 1 , so the maximum value is 400/3.
Because a , b , c > 0 , by A.M.-G.M. inequality we get
a + a b + 3 a b c = a + 2 a ⋅ 4 b + 4 3 a ⋅ 4 b ⋅ 1 6 c .
≤ a + 2 1 ⋅ 2 a + 4 b + 4 1 ⋅ 3 a + 4 b + 1 6 c
≤ 1 2 1 6 a + 1 6 b + 1 6 c
≤ 3 4 0 0
Therefore, since g cd ( 4 0 0 , 3 ) = 1 , the answer is 4 0 0 + 3 = 4 0 3 .
Apply the AM-GM inequality:
a b = ( x a ) ( b x ) ≤ 2 x a + b x = 2 x 1 a + 2 x b 3 a b c = 3 ( y a ) ( z b ) ( c y z ) ≤ 3 y a + z b + c y z = 3 y 1 a + 3 z 1 b + 3 y z c ⇒ a + a b + 3 a b c ≤ ( 1 + 2 x 1 + 3 y 1 ) a + ( 2 x + 3 z 1 ) b + 3 y z c ( ∗ ) where x , y , z > 0
However, because the only given data we have is a + b + c = 1 0 0 , our goal is to find a positive constant k such that a + a b + 3 a b c ≤ k ( a + b + c ) = k a + k b + k c .
So, try to set 1 + 2 x 1 + 3 y 1 = 2 x + 3 z 1 = 3 y z . This yields a very beautiful and comfortable solution: x = 2 , y = 4 , z = 1 .
Plug in again to the inequality ( ∗ ) :
a + ( 2 a ) ( 2 b ) + 3 ( 4 a ) ( 1 b ) ( 4 c ) = a + a b + 3 a b c ≤ 3 4 a + 3 4 b + 3 4 c = 3 4 0 0 .
Equality happen when: 2 a = 2 b a n d 4 a = b = 4 c a n d a + b + c = 1 0 0 ⇒ a = 2 1 1 6 0 0 ; b = 2 1 4 0 0 ; c = 2 1 1 0 0
Moderator note:
Great approach. It is not immediately apparent why the approach would work, and we are mostly hoping that there are variables which allow for it to work out.
Always remember that to show you actually have the maximum , you need to show that equality can exist. Otherwise, all that you have is an upper bound.
For example, it is clear that − x 2 ≤ 0 , − ( x + 1 ) 2 ≤ 0 . However, the maximium of − x 2 − ( x + 1 ) 2 is not 0 + 0 = 0 . In this case, we only have an upper bound, but it is not the lowest upper bound .
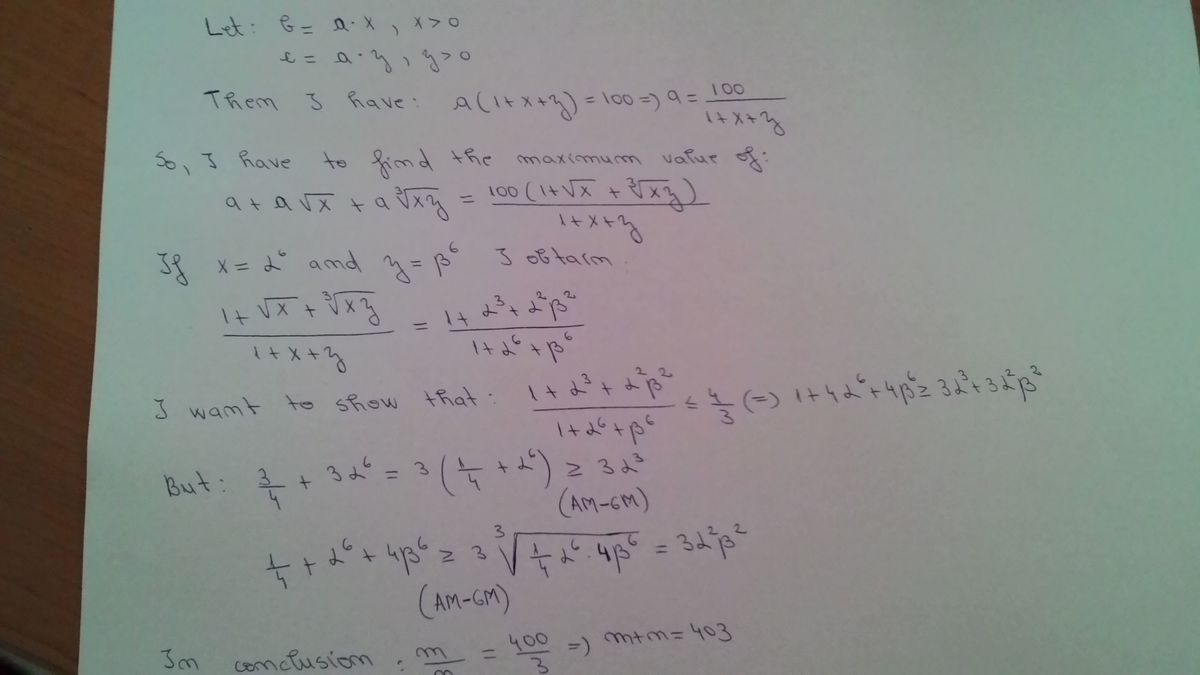
By the AM-GM inequality , we have:
2 a + 4 b 3 a + 4 b + 1 6 c ≥ a ⋅ 4 b ⟹ a b ≤ 4 a + 4 b , ≥ 3 a ⋅ 4 b ⋅ 1 6 c ⟹ 3 a b c ≤ 1 2 a + 4 b + 1 6 c .
Adding these two equations together and an a to both sides, we get:
a + a b + 3 a b c ≤ 3 4 ( a + b + c ) = 3 4 0 0 .
Voila!
From the second equation, equality case holds at a = 4 b = 1 6 c .
For some inspiration on how to discover this approach, check out Anqi Li's solution.