Algebraic Electronics!
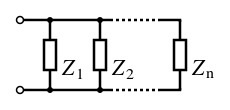 Consider a network Q consisting of 2015 distinct parallel impedances (in ohms)
, such that each of these individual values satisfy the equation
.
Consider a network Q consisting of 2015 distinct parallel impedances (in ohms)
, such that each of these individual values satisfy the equation
.
Determine the total impedance (in ohms) of an impedance network consisting of 2015 Q networks in series.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It is obvious that Z 1 , Z 2 , . . . Z 2 0 1 5 are zeroes of the polynomial y = ( x − 2 ) 2 0 1 5 − 2 2 0 1 7 . Thus, by Vieta's formulas, we can get the net impedance of network Q, which is the quotient of the constant over the coefficient in x (Do you see why?). That is, 2 0 1 5 ⋅ 2 2 0 1 4 2 2 0 1 5 + 2 2 0 1 7 , which simplifies to 4 0 3 2 ohms. Since there are 2 0 1 5 of these in series, we finally get the answer 2 0 1 5 ⋅ 4 0 3 2 = 1 0 .