Algebraic Locks (Set , Problem , Version )
You have an algebraic lock to crack open. They are all different digits from .
You have some clues:
Can you solve the algebraic lock or will the lock outsmart you? Comment in the Discussion about this question (answer as 'the lock outsmarted me' or 'I solved the algebraic lock'.)
Give your answer as the four-digit code to open it (after the algebraic work).
If is fractional (or fractional and negative), round it to the nearest positive integer.
If is negative but not fractional, remove the sign
If the number after inserting the -values is negative, remove the sign.
Hint:
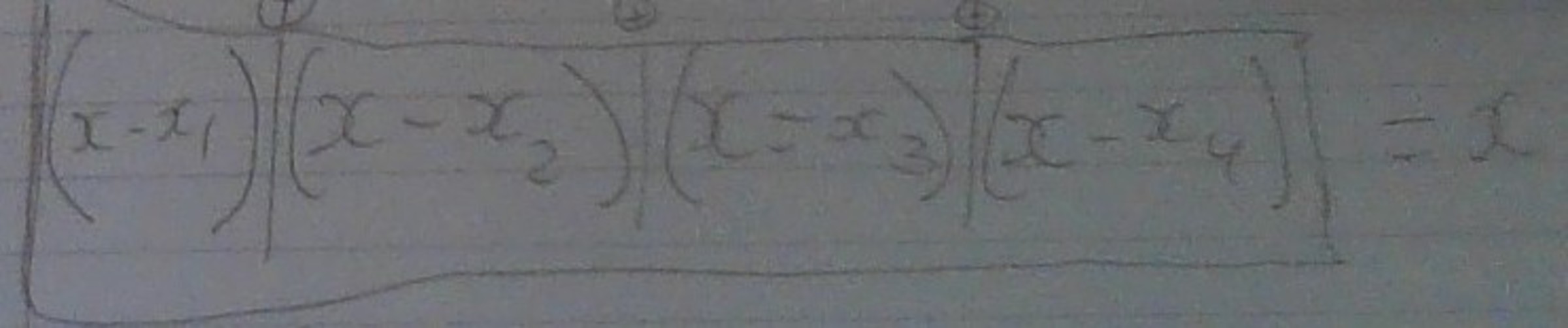
The answer is 2104.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since y 1 + 8 = y 3 , y 1 = 1 , y 3 = 9
Since y 4 + 2 ( y 2 ) = 9 , we need to check all the permutations of the sums of 9 :
1 + 8 = 9
2 + 7 = 9
3 + 6 = 9
4 + 5 = 9
5 + 4 = 9
6 + 3 = 9
7 + 2 = 9
8 + 1 = 9
Since y 4 , y 2 are different digits, we remove the ones that results in the violation of the different digits rule:
1 + 8 = 9
2 + 7 = 9
4 + 5 = 9
5 + 4 = 9
7 + 2 = 9
8 + 1 = 9
Now, we remove the ones that cannot support the 2 ( y 2 ) part of the second clue:
1 + 8 = 9
4 + 5 = 9
5 + 4 = 9
7 + 2 = 9
Now, we remove the ones that reverses the y -values in the second clue:
1 + 8 = 9
5 + 4 = 9
7 + 2 = 9
Now, remove the ones that violate the different digits rule again:
5 + 4 = 9
Therefore y 4 = 5 , y 2 = 2
Now, plug the y -values in:
x + 1 + x − 2 + x + 9 + x − 5 = 4 x + 1 0 − 7 = 4 x + 3 = x
Simplify:
3 x + 3 = 0
3 x = − 3
x = − 1 - remove the − sign - x = 1
Plug x = 1 :
1 + 1 = 2
1 − 2 = − 1 - remove the − sign - 1 − 2 = 1
1 + 9 = 1 0 = 0
1 − 5 = − 4 - remove the − sign - 1 − 5 = 4
Code = 2 1 0 4