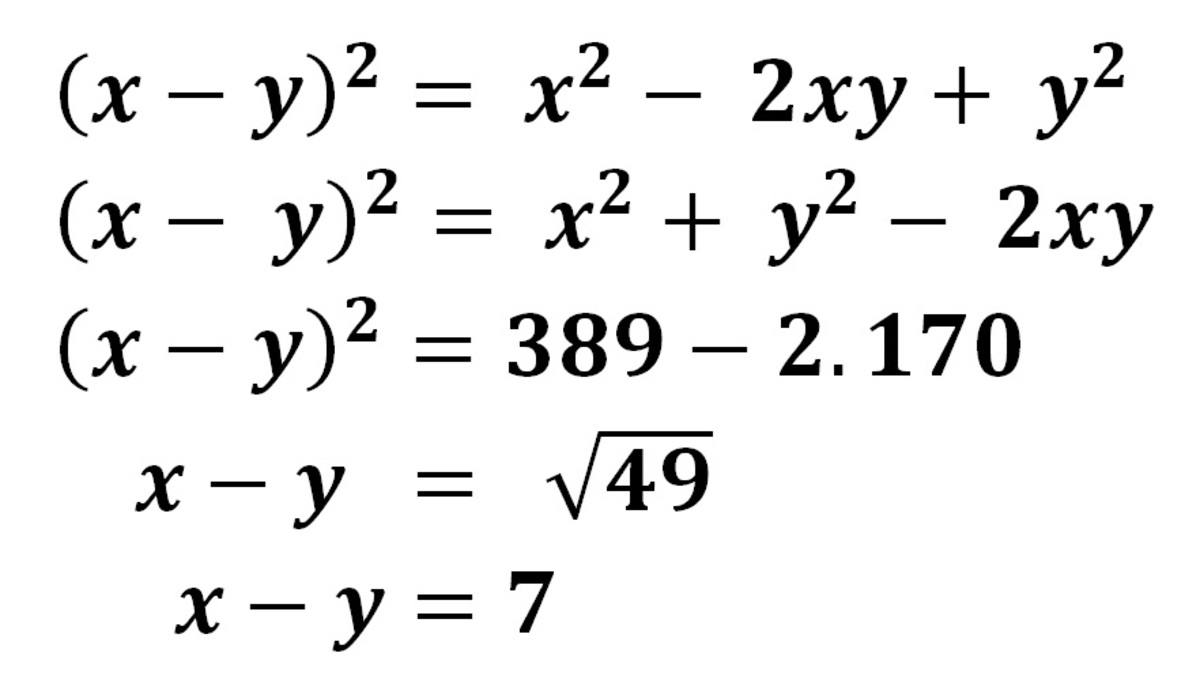Algebraic substitution

$x^2+y^2+2xy=340+389$

$(x+y)^2=729$

$(x+y)=27$

$17 \times 10=170 \rightarrow |x-y|=7$

Given that $x^2 + y^2 = 389$ and $xy = 170$

We can expand it to $x^2 + y^2 - 2xy = 389 - 2(140)$

$(x-y)^2 = 49$ or simply $|x-y|=\boxed{7}$

We can write x^2+y^2 as (x-y)^2+2xy

By substituting the given values, we get

389=(x-y)^2+2(170)

=>389=(x-y)^2+340

=>389-340=(x-y)^2

=>49=>(x-y)^2

=>x-y=49^1/2

=>x-y=7

therefore x-y=7

x^2+y^2 = 389 = (x-y)^2 + 2xy.

xy=170.

thus, (x-y)^2 + 340 = 389.

implies, (x-y)^2 = 49.

thus, (x-y) = 7.

Subtracting twice the second expression from the first, we have

$x^2+y^2-2xy=(x-y)^2=49$

from where it follows that $|x-y|=7$

2(x-y)=x^2+y^2,thus (x-y)2(170)=(x^2+y^2)=389,x-y(340)=x^2+y^2(389)equal to 389-340=49, mean that x-y= square root 49=x-y=7