Alice and Analytic Geometry

Geometry Level 3

In order to defeat Red Queen, Alice has gone through many difficulties and won several battles, and finally made her way towards Red Queen's Palace.

The door of the Palace is locked and needs a password to open. Before the door of the palace, Alice found a paper which says:

The final answer you have sought

After all the battles you have fought

Before Alice's respite

You must solve a problem

And find what hides in the _ _ _ _ _ _ _ _ _ _ _ _s

We have an ellipse

And its directrix

Whose Focus point is on x-axis

We have a line through the right focus point

And meets at two points

Make two projection points to the right directrix

And connect the alternative points

They will always meet at the same point

The _ _ _ _ _ _ _ _ _ _ _ _ is the sum of coefficients and powers of a,b/c

And its y-coordinate

Alice first figured out the blank word is "intersection" since the blank is 12 letters long, and the line means:

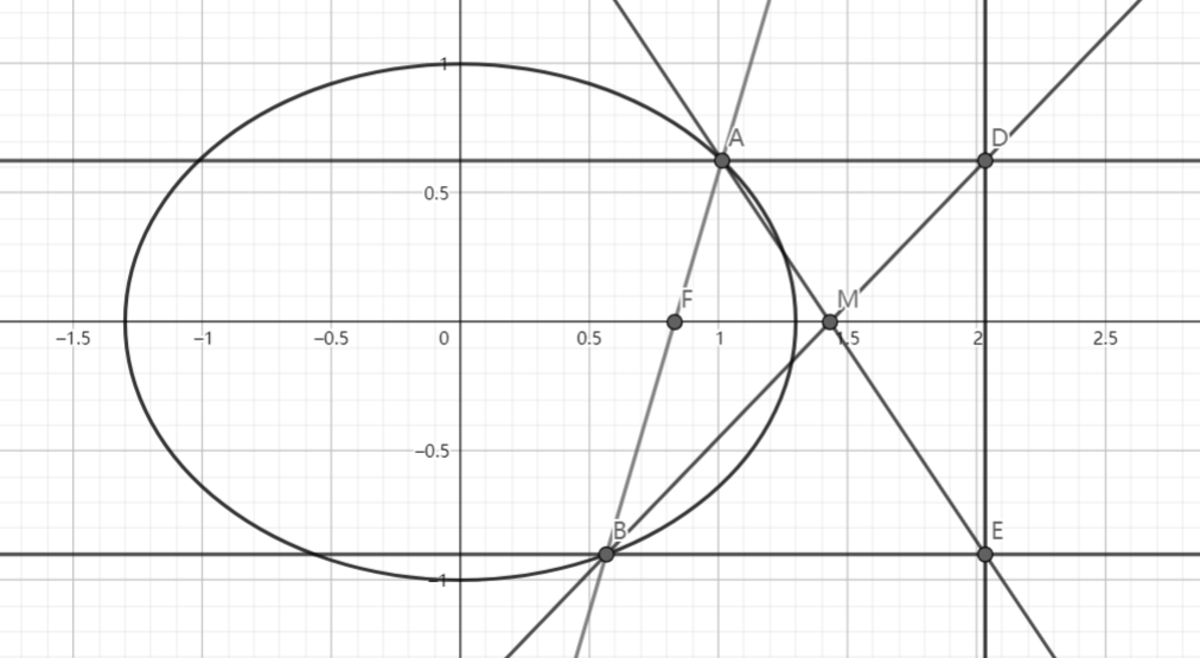
If we have an ellipse with the equation: $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 \ (a>b>0)$ , and a line passing through the right focus point $F(c,0)$ intersects with the ellipse at point $A,B$ , then point $D,E$ are their corresponding projection points to the right directrix. If we connect $AE$ and $BD$ , they will always intersect at the fixed point $(\dfrac{Aa^{B}+Cb^{D}}{Ec^{F}},Y)$ when simplified to its simplest form and $A>0$ . The password to the palace is $A+B+C+D+E+F+Y$ .

This is how far Alice get. Help Alice find the password and make her way towards Red Queen.

This is the picture it means:

The answer is 8.

1 solution

David Vreken
Sep 27, 2019

Let $C$ be the intersection of a line through $F$ perpendicular to $DE$ . Since $AD || BE || FC$ , $\frac{AF}{AB} = \frac{DC}{DE}$ , and also $\triangle ADM \sim \triangle EBM$ by AA similarity, so $\frac{AM}{ME} = \frac{AD}{BE}$ .

By properties of a directrix, $\frac{AD}{BE} = \frac{AF}{FB}$ .

Therefore, $\frac{AM}{ME} = \frac{AD}{BE} = \frac{AF}{FB}$ , therefore $\triangle AFM \sim \triangle DBE$ by SAS similarity, so $FM || BE$ , but since $FC || BE$ , $M$ must lie on $FC$ .

Since $\triangle AFM \sim \triangle ABE$ , $\frac{FM}{AF} = \frac{BE}{AB}$ or $FM = BE \cdot \frac{AF}{AB}$ , and since $MC || BE$ , $\triangle DMC \sim \triangle DBE$ by AA similarity, so $\frac{MC}{DC} = \frac{BE}{ED}$ or $MC = BE \cdot \frac{DC}{ED}$ . But from above we had $\frac{AF}{AB} = \frac{DC}{DE}$ . Therefore, $FM = BE \cdot \frac{AF}{AB} = BE \cdot \frac{DC}{ED} = MC$ or $FM = MC$ , so $M$ is the midpoint between $F$ and $C$ .

By the properties of an ellipse and its directrix, the coordinates of the focus $F$ is $F(c, 0)$ and at point $C$ is $C(\frac{a^2}{c}, 0)$ , so its midpoint $M$ has coordinates of $M(\frac{1}{2}(c + \frac{a^2}{c}), 0)$ or $M(\frac{a^2 + c^2}{2c}, 0)$ . Since in an ellipse $c^2 = a^2 - b^2$ , this can be simplified to $M(\frac{2a^2 - b^2}{2c}, 0)$ .

Therefore, $A = 2$ , $B = 2$ , $C = -1$ , $D = 2$ , $E = 2$ , $F = 1$ , $Y = 0$ , and $A + B + C + D + E + F + Y = \boxed{8}$ .

Alice and Analytic Geometry

The answer is 8.

1 solution

0 pending reports