Alice and Bob Marble Fight - Part 2
Alice and Bob are at either end of a (really long) track. Alice has 30 marbles and Bob has 20 marbles. They send all of their marbles towards each other in quick succession. Whenever 2 marbles collide they will just bounce back and start traveling in the opposite direction.
How many times do the marbles collide?
Assume that the marbles are of the same mass, and that the collisions are perfectly elastic. All marbles move at the same speed.
Image credit: Wikipedia Leonardo Poletto
The answer is 600.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
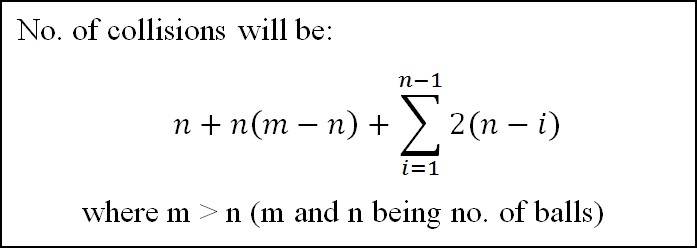
Instead of colliding, let's assume that the marbles simply pass through each other, as the result is identical except for different labels on the marbles which we don't care.
But now there are trivially 3 0 ⋅ 2 0 meetings: each of Alice's marble will meet each of Bob's marble exactly once. The number of meetings must be equal to the number of collisions, as a meeting is essentially a collision, thus there are 3 0 ⋅ 2 0 = 6 0 0 collisions.