Alice in Wonderland - The Phalanx

Probability Level 3

When Alice went into the Wonderland, she saw a very, very large phalanx commanded by Red Queen.

Suppose that the phalanx is formed by $n \times n$ Red soldiers, that is, the phalanx has $n$ rows and $n$ columns.

The coordinate $(i,j)$ means row $i$ , column $j$ , $(1,\_)$ is the frontmost and $(n,\_)$ is the behindmost, $(\_,1)$ is the leftmost and $(\_,n)$ is the rightmost.

In order to manage them, the Red Queen has indexed them from front to behind and left to right, in other words, the index of the Red soldier at position $(i,j)$ is $(i-1)\times n+j$ .

Red Queen loves to command them and move them around.

The command is as follows:

Choose a Red soldier at position $(x,y)$ to leave the phalanx. There will be a gap of the phalanx.
Let all the soldiers on the same row and at the right of the gap move left to fill the gap (without changing their relative position). After the command, the gap is now at $(x,n)$ .
Let all the soldiers on the same column and at the behind of the gap move forward to fill the gap (without changing their relative position). After the command, the gap is now at $(n,n)$ .
Let the soldier who leaves the phalanx fill the gap at $(n,n)$ .

Notice that all the indexes of the soldiers do not change after the commands. After a couple of steps, their indexes may be in random order.

For instance, if Red Queen has a $2 \times 2$ phalanx and she commands the soldier at position $(1,1),(2,2),(1,2)$ , the process is as follows:

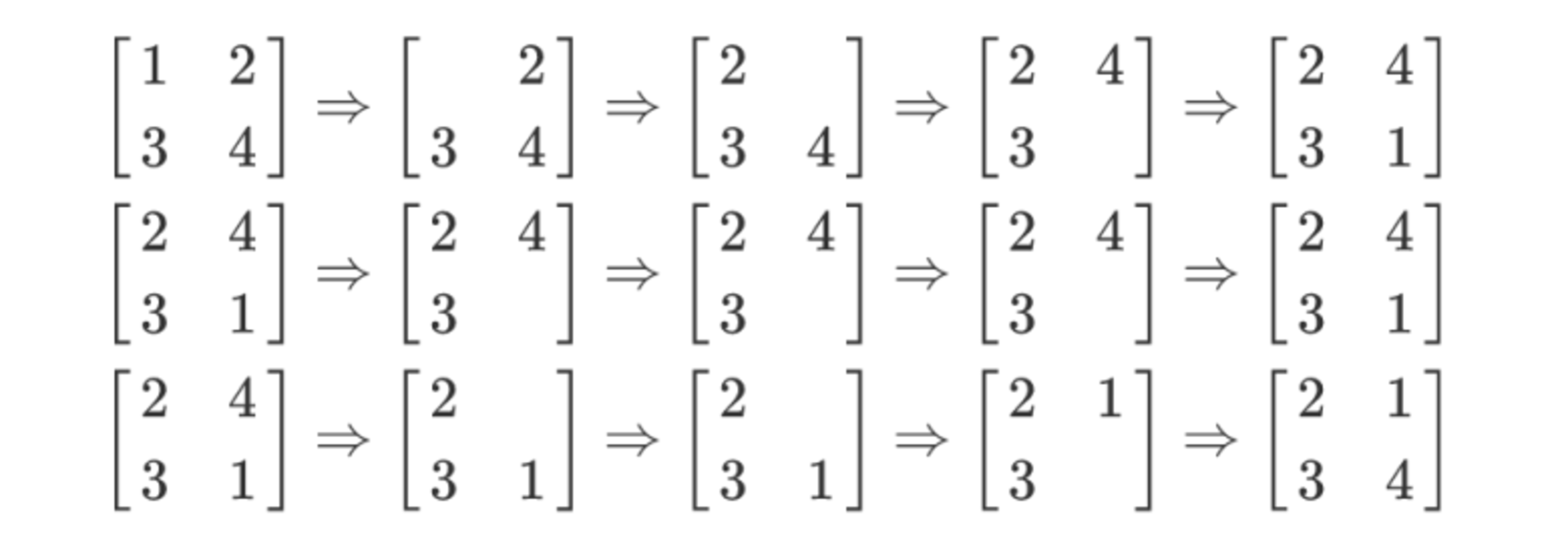
Therefore the soldier at position $(2,2)$ has index $4$ .

One day, Red Queen gathered all her Red soldiers to form a $1000 \times 1000$ phalanx. In order to test their loyalty, she command all of them in order of front to behind and left to right, that is, command the soldier at position $(1,1),(1,2),(1,3),...(1,1000)$ , and then $(2,1),(2,2),(2,3),...(2,1000),...$ until $(1000,1),(1000,2),(1000,3),...(1000,1000)$ .

After all the commands, find the index of the soldier at position $(1000,1000)$ .

Note: Consider the time complexity and memory when using a computer to solve this problem.

The answer is 999977.

1 solution

David Vreken
Oct 3, 2019

Because of the given order of the instructions and the commands, for any $n \times n$ phalanx, the soldiers in the last row (except for the last one) are unaffected until the Red Queen starts calling out orders for that last row. Also, since $1000$ is an even number, whatever soldier is in position $(1000, 1000)$ will not be the final soldier at position $(1000, 1000)$ after the Red Queen calls out orders for the last row. This means that we only need to consider how the last row is affected by the Red Queen's orders to save on computational time.

The following Python computer program that follows the Red Queen's orders for the last row gives an output of $\boxed{999977}$ :

# Alice in Wonderland - The Phalanx
# Python 2.7.3

# Make a list for the last row
n = 1000
p = []
for a in range(n ** 2 - n + 1, n ** 2 + 1):
    p.append(a)

# Perform commands for positions (1000, 1), (1000, 2) ... (1000, 1000)
for a in range(0, len(p)):
    k = p[a]
    p.remove(k)
    p.append(k)

# Print the index of the soldier at (1000, 1000)
print p[n - 1]

For even $n$ , the handy (and natural!) formula $n^2+n+1-2^{\lfloor \log_2 n+1 \rfloor}$ seems to give the result. Umm...can't say I have a proof of this, though - any ideas?

Chris Lewis - 1 year, 8 months ago

Actually, this formula also works for odd $n$ , except those one less than a power of two.

Chris Lewis - 1 year, 8 months ago

Yes, I can see the pattern and that formula, too, but I'm also having trouble proving it. I'll pontificate on a few points that you may or may not have already observed, and maybe one of us will be inspired to prove it...

If we number the last row with $n$ soldiers $(0, 1, 2, ... , n - 1)$ , then we can work out the first few values of $n$ by hand:

$n$	$f(n)$
$1$	$0$
$2$	$0$
$3$	$2$
$4$	$0$
$5$	$2$
$6$	$4$
$7$	$6$
$8$	$0$

When $n$ is a power of $2$ then $f(n) = 0$ , otherwise $f(n)$ increases by increments of $2$ .

Writing this table in binary shows an interesting property that if you take any $n$ and take away the first $1$ and add a $0$ to the end you get $f(n)$ :

$n$	$f(n)$
$0001$	$0000$
$0010$	$0000$
$0011$	$0010$
$0100$	$0000$
$0101$	$0010$
$0110$	$0100$
$0111$	$0110$
$1000$	$0000$

The formula for the tables is $f(n) = 2n - 2^{\lfloor \log_2n + 1 \rfloor}$ . For the Red Queen's army, the last row starts with the number $n^2 - n + 1$ , so the result is the equation you came up with which is $n^2 + n + 1 - 2^{\lfloor \log_2n + 1 \rfloor}$ .

The problem is that I can only show that the equation works by seeing the pattern, not deductively.

David Vreken - 1 year, 8 months ago

Alice in Wonderland - The Phalanx

The answer is 999977.

1 solution

0 pending reports