All About Geometry
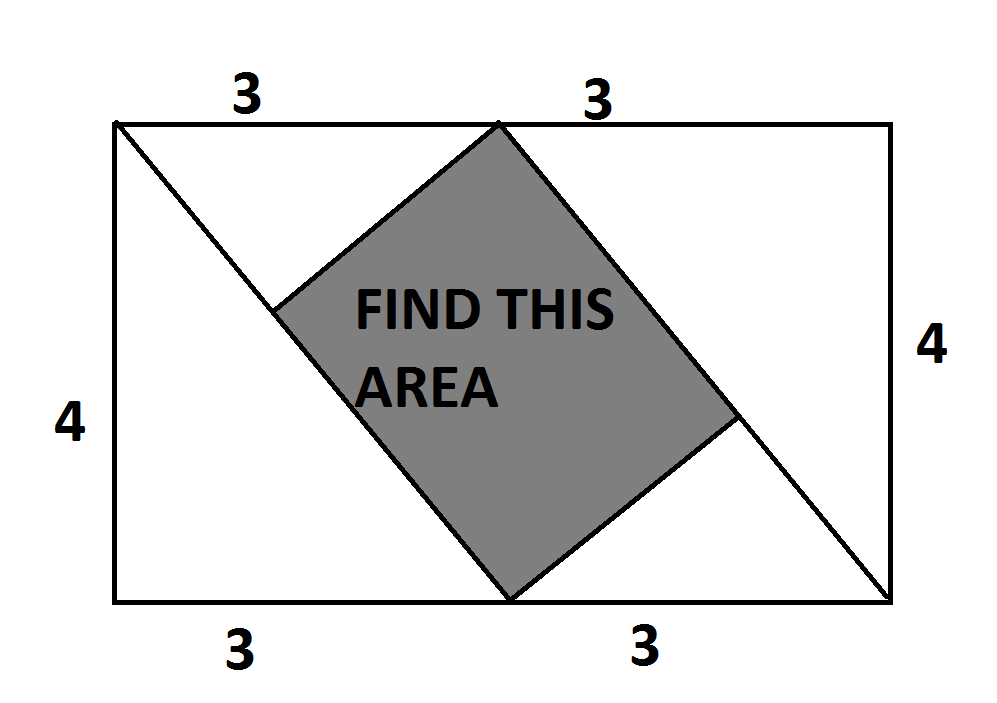 Find the shaded area.
Find the shaded area.
Note: The shaded area is a rectangle.
The answer is 7.68.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
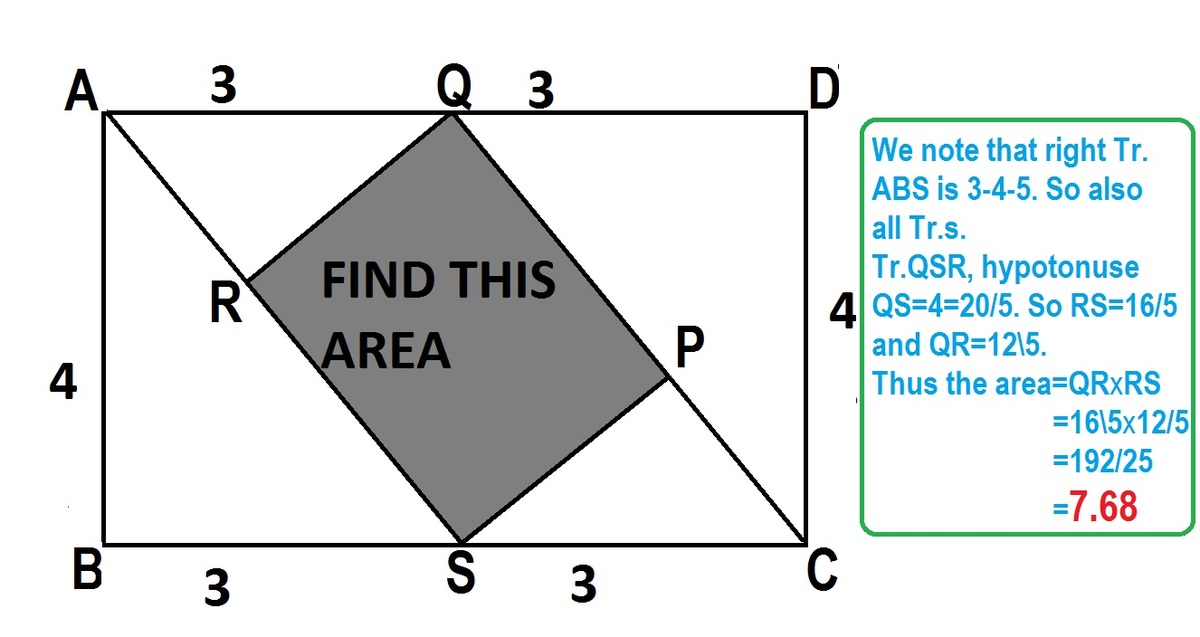
i was thinking a bit differently, if i push tr. SPC to join AQR it will form a ||gm if i find area of this ||gm and subtract it from 24 i would get the answer but i colud'nt calculate it's area (||gm) can you help?
 solution
solution
In triangle PBC.
Using pythagoras theorem, we get
P
C
=
5
P Q = B C = A D = 4
In triangle P Q C .
Using similarity.
A B A E = B C E B = A C A B
4 A E = 3 E B = 5 4
We get, A E = 5 1 6 and E B = 5 1 2
Therefore, area of shaded part= 5 1 6 × 5 1 2 = 7 . 6 8
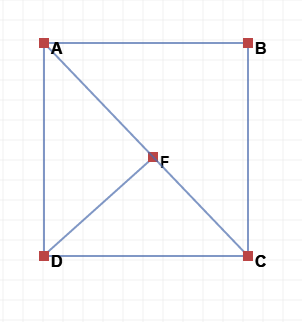 The Main Objective of the Question is to find the Area of smaller Triangles.I am concentrating on the second half of the Figure , we need to find Area of
△
D
F
C
.Now Observe that
∠
C
A
B
and
∠
A
C
D
are equal. Let
∠
C
A
B
=
∠
A
C
D
=
θ
Using Trigonometry
The Main Objective of the Question is to find the Area of smaller Triangles.I am concentrating on the second half of the Figure , we need to find Area of
△
D
F
C
.Now Observe that
∠
C
A
B
and
∠
A
C
D
are equal. Let
∠
C
A
B
=
∠
A
C
D
=
θ
Using Trigonometry
cos θ = A C A B = 5 3 = D C F C ⟹ F C = 5 9 sin θ = A C B C = 5 4 = D C D F ⟹ D F = 5 1 2 Area of △ D F C = 2 1 × D F × F C = 5 0 1 0 8 Shaded Area = Total Area − 2 × ( A r . △ A B C + A r . △ D F C ) ⟹ A r e a = 2 4 − 2 × ( 6 + 5 0 1 0 8 ) ⟹ 1 2 − 4 . 3 2 = 7 . 6 8
NOTE: Due to symmetry i was concentrating on the 2nd half of the figure , because the same process can be done on the first part