All Angles!

Geometry Level pending

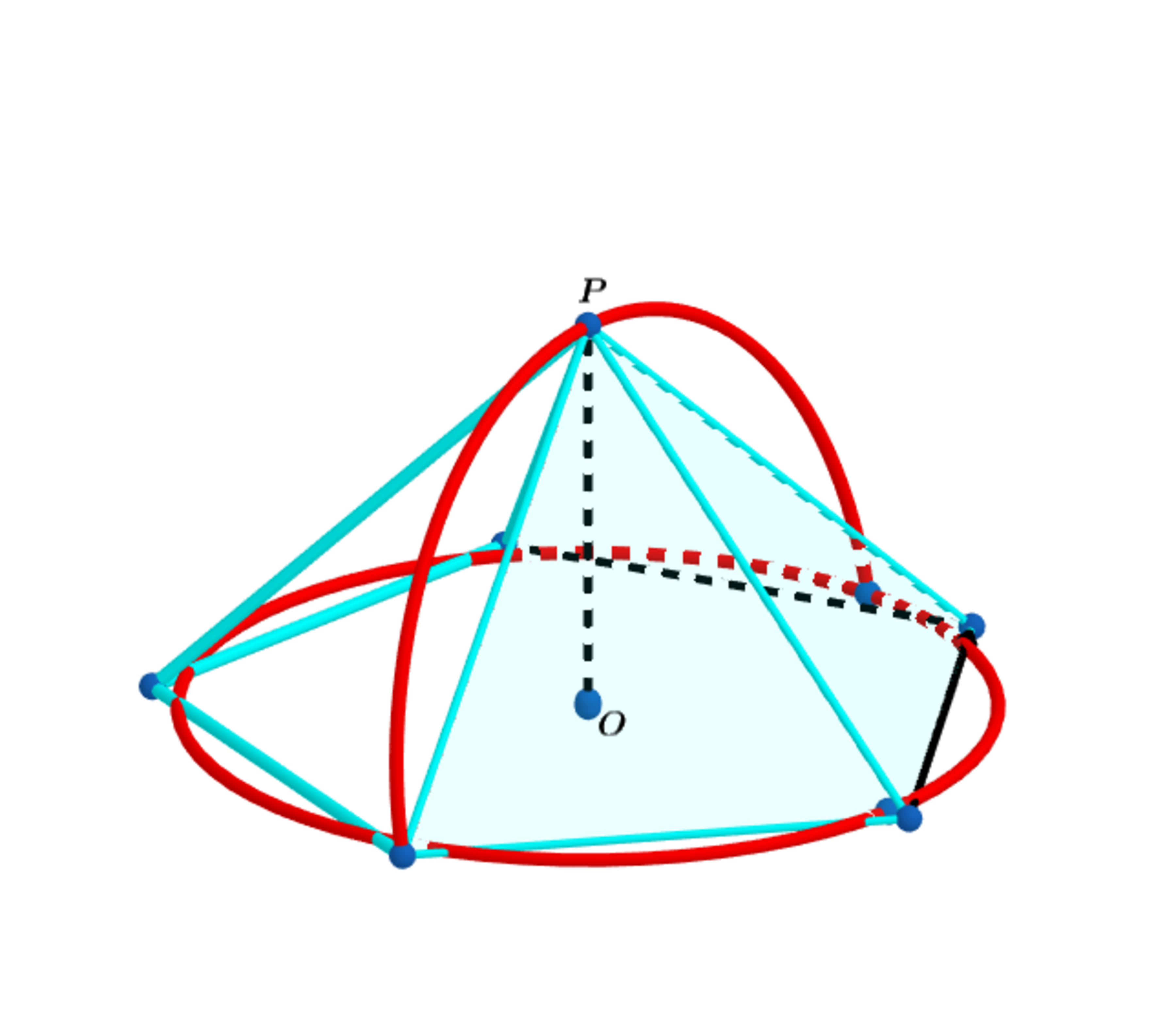
Extend the above diagram to a pyramid whose base is a regular n n -gon.

Let O O be the center of the regular n n - gon and construct a circle centered at O O whose circumference is equal to the perimeter of the n n -gon. Folding the arc of the semi-circle at a right angle, as shown above, the radius of the semicircle becomes the height of the n n -gonal pyramid.

Let θ n \theta_{n} be the obtuse angle made between two adjacent faces, s n s_{n} the slant height and e n e_{n} the edge angle.

  1. Find cos ⁡ ( θ n ) \cos(\theta_{n}) , tan ⁡ ( s n ) \tan(s_{n}) and tan ⁡ ( e n ) \tan(e_{n}) .
  2. Using n = 13 n = 13 find the sum of the obtuse angle made between two adjacent faces and the slant height angle and the edge angle (in degrees).


The answer is 250.607632797217.

Rocco Dalto by Rocco Dalto , 67, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Rocco Dalto
Jan 2, 2021

Let each radii of the regular n n -gon be a a and A ( 0 , 0 , 0 ) , B ( a cos ⁡ ( 2 π n ) , − a sin ⁡ ( 2 π n ) , 0 ) , C ( a cos ⁡ ( 2 π n ) , a sin ⁡ ( 2 π n ) , 0 ) A(0,0,0), B(a\cos(\dfrac{2\pi}{n}), -a\sin(\dfrac{2\pi}{n}),0), C(a\cos(\dfrac{2\pi}{n}), a\sin(\dfrac{2\pi}{n}),0) and P ( 0 , 0 , r ) P(0,0,r) .

A B ⃗ = − 2 a sin ⁡ 2 ( π n ) i ⃗ − a sin ⁡ ( 2 π n ) j ⃗ + 0 k ⃗ \vec{AB} = -2a\sin^2(\dfrac{\pi}{n})\vec{i} - a\sin(\dfrac{2\pi}{n})\vec{j} + 0\vec{k}

A C ⃗ = − 2 a sin ⁡ 2 ( π n ) i ⃗ + a sin ⁡ ( 2 π n ) j ⃗ + 0 k ⃗ \vec{AC} = -2a\sin^2(\dfrac{\pi}{n})\vec{i} + a\sin(\dfrac{2\pi}{n})\vec{j} + 0\vec{k}

A P ⃗ = − a i ⃗ + 0 j ⃗ + r k ⃗ \vec{AP} = -a\vec{i} + 0\vec{j} + r\vec{k}

⟹ u ⃗ = A P ⃗ X A C ⃗ = − a r sin ⁡ ( 2 π n ) i ⃗ − 2 a r sin ⁡ 2 ( π n ) j ⃗ − a 2 sin ⁡ ( 2 π n ) k ⃗ \implies \vec{u} = \vec{AP} X \vec{AC} = -ar\sin(\dfrac{2\pi}{n})\vec{i} - 2ar\sin^2(\dfrac{\pi}{n})\vec{j} - a^2\sin(\dfrac{2\pi}{n})\vec{k}

and

v ⃗ = A P ⃗ X A C ⃗ = a r sin ⁡ ( 2 π n ) i ⃗ − 2 a r sin ⁡ 2 ( π n ) j ⃗ + a 2 sin ⁡ ( 2 π n ) k ⃗ \vec{v} = \vec{AP} X \vec{AC} = ar\sin(\dfrac{2\pi}{n})\vec{i} - 2ar\sin^2(\dfrac{\pi}{n})\vec{j} + a^2\sin(\dfrac{2\pi}{n})\vec{k}

⟹ u ⃗ ⋅ v ⃗ = 4 a 2 sin ⁡ 2 ( π n ) ( ( 2 r 2 + a 2 ) sin ⁡ 2 ( π n ) − ( r 2 + a 2 ) ) \implies \vec{u} \cdot \vec{v} = 4a^2\sin^2(\dfrac{\pi}{n})((2r^2 + a^2)\sin^2(\dfrac{\pi}{n}) - (r^2 + a^2))

and

∣ u ⃗ ∣ 2 = ∣ v ⃗ ∣ 2 = 4 a 2 sin ⁡ 2 ( π n ) ( ( r 2 + a 2 ) − a 2 sin ⁡ 2 ( π n ) ) |\vec{u}|^2 = |\vec{v}|^2 = 4a^2\sin^2(\dfrac{\pi}{n})((r^2 + a^2) - a^2\sin^2(\dfrac{\pi}{n}))

⟹ cos ⁡ ( θ n ) = u ⃗ ⋅ v ⃗ ∣ u ⃗ ∣ 2 = \implies \cos(\theta_{n}) = \dfrac{\vec{u} \cdot \vec{v}}{|\vec{u}|^2} = ( 2 r 2 + a 2 ) sin ⁡ 2 ( π n ) − ( r 2 + a 2 ) ( r 2 + a 2 ) − a 2 sin ⁡ 2 ( π n ) \dfrac{(2r^2 + a^2)\sin^2(\dfrac{\pi}{n}) - (r^2 + a^2)}{(r^2 + a^2) - a^2\sin^2(\dfrac{\pi}{n})}

Let a ∗ a^{*} be length of each side of the n n -gon ⟹ a ∗ = 2 a sin ⁡ ( π n ) \implies a^{*} = 2a\sin(\dfrac{\pi}{n})

and n a ∗ = 2 π r ⟹ r = n a ∗ 2 π = a n sin ⁡ ( π n ) π ⟹ na^{*} = 2\pi r \implies r = \dfrac{na^{*}}{2\pi} = \dfrac{an\sin(\dfrac{\pi}{n})}{\pi} \implies

cos ⁡ ( θ n ) = ( sin ⁡ 2 ( π n ) ) ( 2 n 2 sin ⁡ 2 ( π n ) + π 2 − n 2 ) − π 2 ( n 2 − π 2 ) sin ⁡ 2 ( π n ) + π 2 \cos(\theta_{n}) = \dfrac{(\sin^2(\dfrac{\pi}{n}))(2n^2\sin^2(\dfrac{\pi}{n}) + \pi^2 - n^2) - \pi^2}{(n^2 - \pi^2)\sin^2(\dfrac{\pi}{n}) + \pi^2}

⟹ cos ⁡ ( θ 13 ) ≈ − 0.9415978180419575 ⟹ θ 13 ≈ 160.321643935123 \implies \cos(\theta_{13}) \approx -0.9415978180419575 \implies \theta_{13} \approx \boxed{160.321643935123} .

The height of one of the congruent triangles of the n n -gon is h ∗ = a cos ⁡ ( π n ) ⟹ tan ⁡ ( s n ) = r h ∗ = n π tan ⁡ ( π n ) h^{*} = a\cos(\dfrac{\pi}{n}) \implies \tan(s_{n}) = \dfrac{r}{h^{*}} = \dfrac{n}{\pi}\tan(\dfrac{\pi}{n})

and tan ⁡ ( e n ) = r a = n π sin ⁡ ( π n ) \tan(e_{n}) = \dfrac{r}{a} = \dfrac{n}{\pi}\sin(\dfrac{\pi}{n})

⟹ s 13 ≈ 45.56536884767 1 ∘ \implies s_{13} \approx \boxed{45.565368847671^{\circ}} and e 13 ≈ 44.72062001442 3 ∘ e_{13} \approx \boxed{44.720620014423^{\circ}}

⟹ θ 13 + s 13 + e 13 ≈ 250.60763279721 7 ∘ \implies \theta_{13} + s_{13} + e_{13} \approx \boxed{250.607632797217^{\circ}} .

Note: Using the inequality cos ⁡ ( x ) < sin ⁡ ( x ) x < 1 \cos(x) < \dfrac{\sin(x)}{x} < 1 ⟹ cos ⁡ ( π n ) < n π sin ⁡ ( π n ) < 1 \implies \cos(\dfrac{\pi}{n}) < \dfrac{n}{\pi}\sin(\dfrac{\pi}{n}) < 1

⟹ lim ⁡ n → ∞ tan ⁡ ( s n ) = lim ⁡ n → ∞ tan ⁡ ( e n ) = 1 \implies \lim_{n \rightarrow \infty} \tan(s_{n}) = \lim_{n \rightarrow \infty} \tan(e_{n}) = 1 and lim ⁡ n → ∞ cos ⁡ ( θ n ) = − 1 \lim_{n \rightarrow \infty} \cos(\theta_{n}) = -1 as it should be.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...