All are 6-digit numbers with the same 6 digits

Computer Science Level 4

Given that A A is a 6-digit number and that 5 A 2 \dfrac{5A}{2} , 3 A 3A , 7 A 2 \dfrac{7A}{2} , 4 A 4A and 11 A 2 \dfrac{11A}{2} are all 6-digit numbers with the same 6 digits as A A . Find A A .


The answer is 153846.

Chan Lye Lee by Chan Lye Lee , 44, Singapore

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

6 solutions

Julien Marcuse
Jun 5, 2018

My Java solution: 

import java.util.ArrayList;
public class Main {

     public static void main(String []args) {
        for (int i = 1; i <= 999999; i++) {
            ArrayList<Integer> digits = digits(i);
            if (!digits.containsAll(digits((5 * i) / 2))) {
                continue;
            }
            if (!digits.containsAll(digits(3 * i))) {
                continue;
            }
            if (!digits.containsAll(digits((7 * i) / 2))) {
                continue;
            }
            if (!digits.containsAll(digits((11 * i) / 2))) {
                continue;
            }
            if (!digits.containsAll(digits(4 * i))) {
                continue;
            }
            System.out.println(i);
        }
     }

     private static ArrayList<Integer> digits(int num) {
         ArrayList<Integer> digits = new ArrayList<>();
         while (num > 0) {
             digits.add(num % 10);
             num /= 10;
         }
         return digits;
     }
}
1 Helpful 0 Interesting 0 Brilliant 0 Confused

Is there a way to optimize?

Robert Tobio - 3 years ago

Am I the only one who thinks that a 6-digit number that satisfies all of this is cool?

Sanchit Sharma - 2 months, 1 week ago
Krutarth Patel
May 28, 2016 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
 
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;

int main()
{
    for (int i = 100000; i <= 999999; i += 2)
    {
        string s, s1, s2, s3, s4;
        s = to_string(i), s1 = to_string((i << 1) + (i >> 1)), s2 = to_string((i << 1) + i), s3 = to_string(i << 2), s4 = to_string((i << 2) + i + (i >> 1));
        sort(s.begin(), s.end()), sort(s1.begin(), s1.end()), sort(s2.begin(), s2.end()), sort(s3.begin(), s3.end()), sort(s4.begin(), s4.end());
        if (s == s1 && s1 == s2 && s2 == s3 && s3 == s4)
        {
            cout << i << "\n";
            break;
        }
    }
    return 0;
}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

If this were to require more calculations, you could reduce the upper bound to 1,000,000*2/11.

First Last - 4 years, 6 months ago

I screened as I progressed. I realized that the initial number had to be between 100000 and 181818 and only even integers needed to be tested.

Do [ d1 = Sort [ IntegerDigits [ i ] ] ; j = 5 i 2 ; d2 = Sort [ IntegerDigits [ j ] ] ; If [ d1 = d2 , j = 3 i ; d2 = Sort [ IntegerDigits [ j ] ] ; If [ d1 = d2 , j = 7 i 2 ; d2 = Sort [ IntegerDigits [ j ] ] ; If [ d1 = d2 , j = 4 i ; d2 = Sort [ IntegerDigits [ j ] ] ; If [ d1 = d2 , j = 11 i 2 ; d2 = Sort [ IntegerDigits [ j ] ] ; If [ d1 = d2 , Print [ i ] ] ] ] ] ] , { i , 100000 , 181818 , 2 } ] ⟹ 153846 \text{Do}\left[\text{d1}=\text{Sort}[\text{IntegerDigits}[i]]; \\ j=\frac{5 i}{2};\text{d2}=\text{Sort}[\text{IntegerDigits}[j]]; \\ \text{If}\left[\text{d1}=\text{d2}, \\ j=3 i;\text{d2}=\text{Sort}[\text{IntegerDigits}[j]]; \\ \text{If}\left[\text{d1}=\text{d2}, \\ j=\frac{7 i}{2};\text{d2}=\text{Sort}[\text{IntegerDigits}[j]]; \\ \text{If}\left[\text{d1}=\text{d2}, \\ j=4 i;\text{d2}=\text{Sort}[\text{IntegerDigits}[j]]; \\ \text{If}\left[\text{d1}=\text{d2}, \\ j=\frac{11 i}{2};\text{d2}=\text{Sort}[\text{IntegerDigits}[j]]; \\ \text{If}[\text{d1}=\text{d2}, \\ \text{Print}[i]]\right]\right]\right]\right], \\ \{i,100000,181818,2\}\right] \Longrightarrow 153846 .

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Vlad Vasilescu
Jul 8, 2018

A not so brief Python solution :

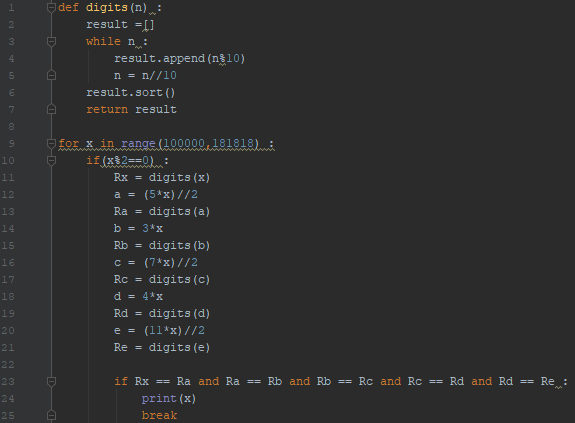
0 Helpful 0 Interesting 0 Brilliant 0 Confused

Is there any solution which does not use programming I tried my best but could not find any such solution.

Srikanth Tupurani - 2 years, 8 months ago
Eric Schneider
Jun 14, 2018

The range is bounded by the minimal 6-digit number (1000000) and the maximal number for which 11 A 2 \frac{11A}{2} is 6-digits (181818). A pythonic solution is implemented below. 

1
 
print(sum([i if i%2==0and[sorted(str(x))for x in[i,5*i//2,3*i,7*i//2,4*i,11*i//2]].count(sorted(str(i)))==6else 0for i in range(100000,181819)]))

I love Python.

Running this program gives the result of 153846 \boxed{153846} .

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Zeeshan Ali
Jun 3, 2018 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
 
import itertools # https://docs.python.org/2/library/itertools.html#itertools.product
import numpy as np # http://www.numpy.org/

# set of all the possible 9 non-zero-digit numbers in acending order
product = list(itertools.product(range(10), repeat=6))

# exclude all those six-digit numbers starting with zero
product = [p for p in product if p[0]]

for p in product: # for every p = (a, b, c, d, e, f) in above set
    q = int(str(p[0])+str(p[1])+str(p[2])+str(p[3])+str(p[4])+str(p[5])) # A
    if (str(np.unique([int(x) for x in str(5*q//2)])) == str(np.unique([int(x) for x in str(3*q)]))
        and str(np.unique([int(x) for x in str(3*q)])) == str(np.unique([int(x) for x in str(7*q//2)]))
        and str(np.unique([int(x) for x in str(7*q//2)])) == str(np.unique([int(x) for x in str(4*q)]))
        and str(np.unique([int(x) for x in str(4*q)])) == str(np.unique([int(x) for x in str(11*q//2)]))):
        print (q) # print the elements or digits of that number 'p'
        break

153846

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...