All curves
The beige shape pictured is comprised of 8 arcs of unit radius. A B = B C = 2 2 and ∠ A B C = 1 3 5 ∘
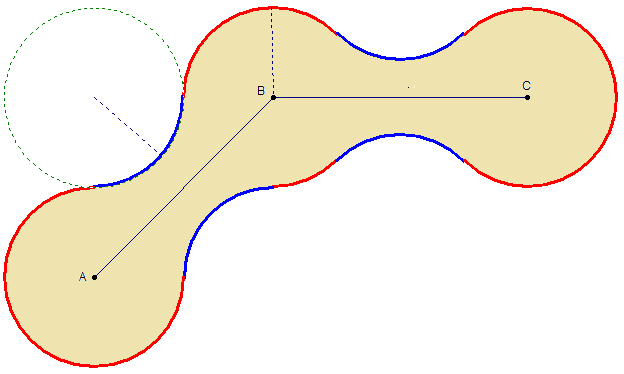
FInd the area of the shape.
The answer is 11.1415925.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The shape can be subdivided into 3 sets of congruent shapes:
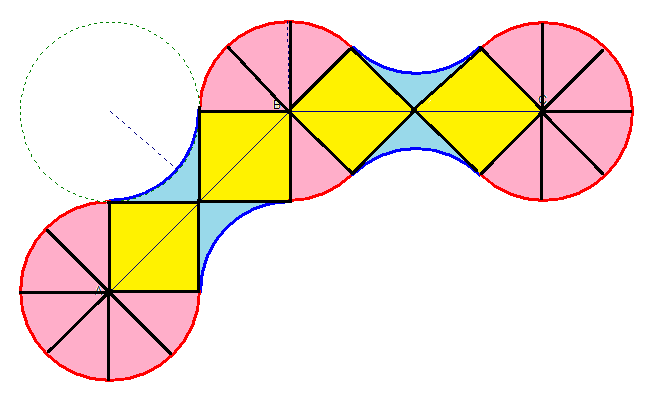
There are 1 6 pink shapes that are 8 1 unit circles for an area of 1 6 ⋅ 8 1 π ⋅ 1 2 = 2 π .
There are 4 blue shapes that are the difference between a unit square and a 4 1 unit circle for an area of 4 ( 1 − 4 1 π ⋅ 1 2 ) = 4 − π .
There are 4 yellow shapes that are unit squares for an area of 4 ⋅ 1 2 = 4 .
This gives a total area of 2 π + 4 − π + 4 = 8 + π ≈ 1 1 . 1 4 1 5 9 2 5 .
The angle is a bit of a red herring. Changing it will not alter the area of the shape (unless it is too small.) Change it to 180 degrees and color as so:
We see the light blue segments can be moved to the light green to form four green squares each of area 2 2 = 2 . The red segment on one end can move to the other side to complete a single circle of unit radius.
Total area: 8 + π ≈ 1 1 . 1 4 1 5 9 2 6 5