This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Moderator note:
Yes, finding the area by "complement" is the easiest way to approach this problem. It would be better to explain how you get the values of 3 , 1 5 , 1 6 unit squared.
Addendum: Great work! Now try Part 2 and Part 3.
Just edited, thanks.
please explain how u got the sides of traingle as 3 and 2 where AB is hypotenuse.
Log in to reply
Just count the squares..:P
each box is 1 unit!!
Area of AB has a max of 3 rows & 2 cols
Using the Pick's formula A r e a = 1 2 + 6 / 2 − 1 = 1 4
can u elaborate on pick's formula
It can be solved by means of coordinate geometry.Along X axis and Y axis respectively A(3,6),B(0,4) and C(8,0).then using the formula for determining area in coordinate geometry which is: 0.5(x1y2+x2y3+x3y4-x2y1-x3y2-x4y3) we can determine the area of the inscribed triangle.
Shoelace formula to the rescue.
Start with the area of the rectangle, 6x8=48 then subtract the areas of the right angled triangles in the corners.
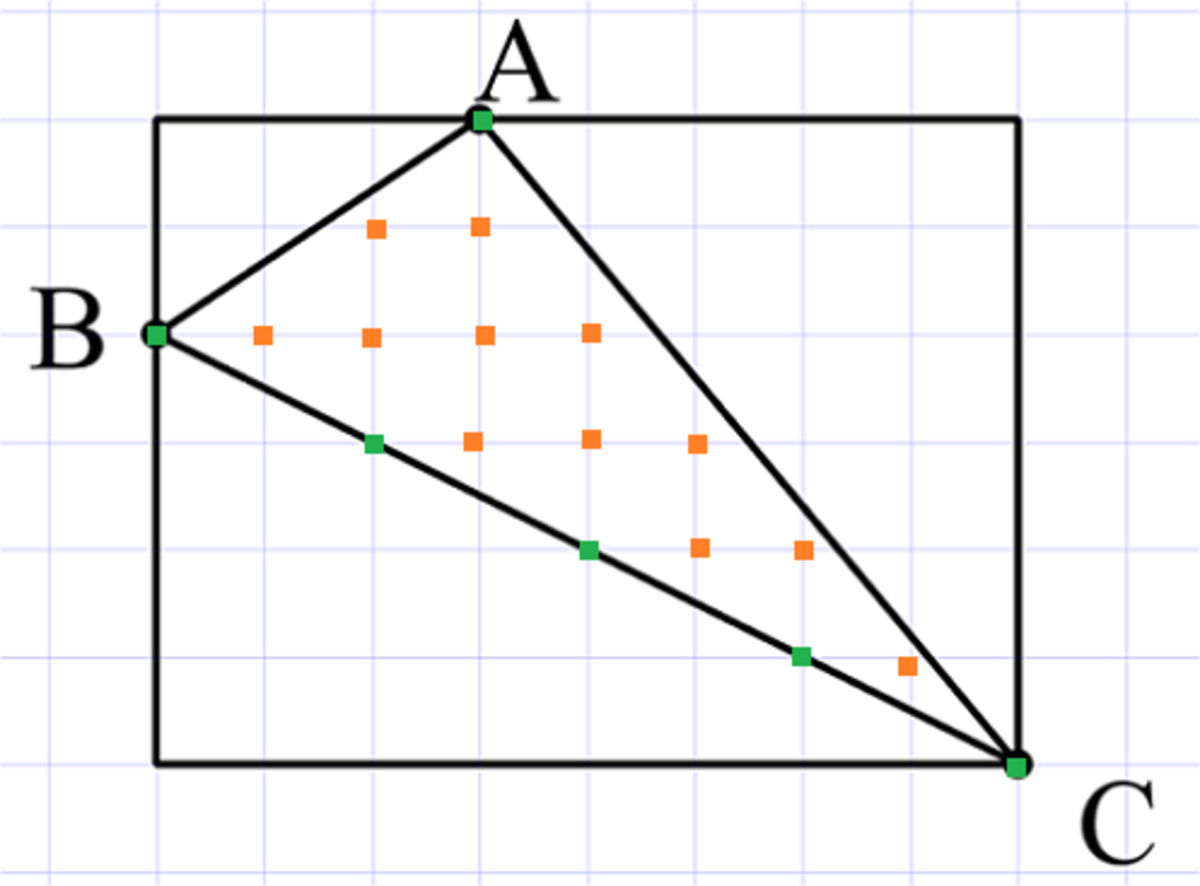
Interior points (Colored Orange = 12) -> i
Border points (Colored Green = 6) -> b
Area = i + 0.5b -1 = 12 + 3 -1 = 14
I used the Shoelace Formula:
Suppose the points are on a Cartesian plane. Then we can represent the points as A = ( 3 , 6 ) , B = ( 0 , 4 ) , C = ( 8 , 0 ) . Then the Shoelace formula gives us:
A r e a = 2 1 ∣ ( 3 ∗ 4 − 6 ∗ 0 ) + ( 0 ∗ 0 − 8 ∗ 4 ) + ( 8 ∗ 6 − 0 ∗ 3 ) ∣ = 1 4
i simply don't have any idea... i just starred at the pic for a while and guessed area of triangle approximately occupies 30% of rectangular area. it gave me 14.4 but i answered 14... luckily that was ryt :D
Do you know why the area must be an integer, or half of an integer? If your approximation is correct, that will further tell you that the answer is 14 or 14.4 or 15!
Found the hypotenuse for each triangle on the outside which gave me the insides coordinates. From there i calculated the area as if it were a rectangle. Then simply divided it by 2. Mathematics brought to you by stoner chris
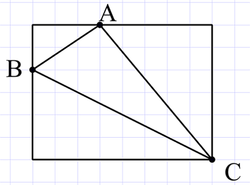
The area of the rectangle is 4 8 u n i t s 2 .
The triangle with hypotenuse AB has area 3 × 2 × 2 1 = 3 u n i t s 2 .
The triangle with hypotenuse AC has area 5 × 6 × 2 1 = 1 5 u n i t s 2 .
The triangle with hypotenuse BC has area 4 × 8 × 2 1 = 1 6 u n i t s 2 .
Then by subtracting the other triangle areas we get 4 8 − 1 5 − 1 6 − 3 = 1 4 u n i t s 2 .