All Roads Should Lead
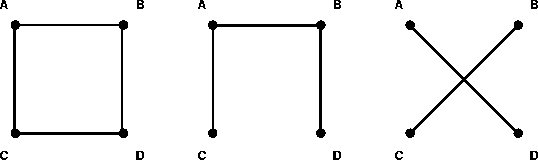In the country of Geometra, there are four towns A, B, C and D that lie on the corners of a ten kilometre square. The government decided to link all the towns with roads. Because of shortage of money, it was desirable to have a road network with the least total length. Proposals were invited and three of the proposals are shown above.
The first proposal is of 40 km length, the second of 30 and the third gives a solution with 28.3 km of road. The designers approved the third plan, but the finance minister sent it back accusing the designers of extravagance. He claimed that a better solution should exist. But, the minister was an old chap and may be wrong.
What is the shortest total length of road that would connect the four towns? Give your answer in metres, approximated to the nearest metre.
The answer is 27321.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The shortest path would have a structure as shown below.
The total length in kilometers can be calculated as (4 times length of diagonal road + length of 'vertical' road)
d = 4 × 5 sec ( 3 π ) + ( 1 0 − 2 × 5 cot ( 3 π ) ) = 2 7 . 3 2 0 5 0 8 k m
Converting into metres, the value to metres would give the answer as 2 7 3 2 0 . 5 0 8 ≈ 2 7 3 2 1 m
See : Steiner Tree