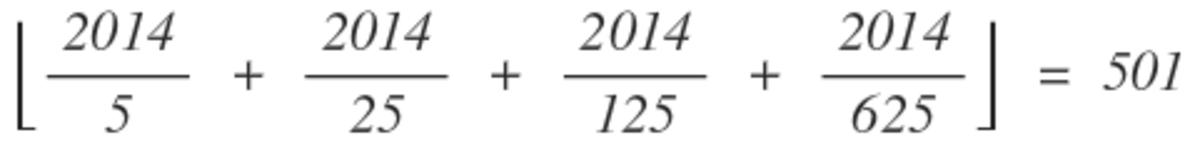All zebra
Number Theory
Level
3
Let
How many zeros are at the end of the decimal representation of
?
The answer is 501.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Only the number of trailing zeros in 2014! is relevant, since the subsequent numbers will all have a greater number of trailing zeros. Number of trailing zeros in 2014! can be obtained by dividing 2014 with the powers of 5: