Almost A Magic Square
Place distinct digits from 1 to 9 in the boxes so that the sums of 3 digits along any of the 4 colored lines are all equal.
What is the maximum possible sum that can be achieved?
For example, using the values in the magic square gives us a sum of 15 along each colored line. Can we do better?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
I like your observation that we must have m = 1 , 5 , 9 :)
I didn't realize that when I wrote this up. Maybe, by selecting a different set of numbers, we could make that observation crucial to solving the problem.
Log in to reply
As long as the nine numbers are evenly spaced integers, any solution will have m equal to the least, middle, or greatest value.
I really liked your clear, logical reasoning. Cheers.
Same way! :)
Brilliant! One question: how did you know that m has to be one more than a multiple of four?
Log in to reply
Because 4 S = 3 m + 4 5 , and S is an integer, I know that 3 m + 4 5 must be a multiple of four. The number 4 5 is one more than a multiple of four, so 3 m should be one less (or, in other words, three more) than a multiple of four. Finally, if 3 m is three more than a multiple of four, then m is one more than a multiple of four.
This is an example of arithmetic modulo 4. In symbolic notation, 4 S ≡ 3 m + 4 5 mod 4 ; 0 ⋅ S ≡ ( − 1 ) ⋅ m + 1 mod 4 ; 0 ≡ 1 − m mod 4 ; m ≡ 1 mod 4 .
I didn't even realize there were four lines >.> I assumed it meant for ALL vertical, horizontal, and diagonal sums to be equal x.x .... so I just did sum (1 thru 9) * 3 since every box is used 3 times except the middle one. Then assumed the middle is the highest number - 9. And got (135+9)/9=18.
Log in to reply
Is it possible to construct a square whose sum of each row, column and diagonal is 18?
By using Gauss' number paring Trick we can easily solve the problem without any algebraic equations.
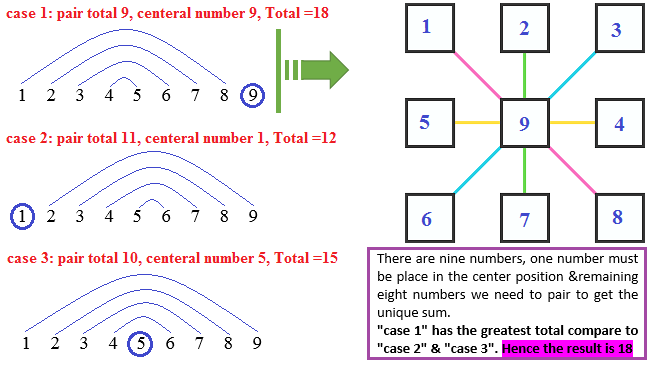
But why does this algorithm work? Can you provide the motivation?
Log in to reply
I updated solution with possible cases how the algorithm works.
I see how you did that, but what are the LOGICAL steps? Could you please elaborate a bit? I am sure it has to do with integers, but I just cannot verbalize what prompted you to organize the numbers in the first place. Thanks.
Log in to reply
My take on his logic is like this: if you want to maximize the sum, 9 should be até the center. You then have to pair each of 8 remaining number such that their respective sums are the same, you can do that if you order then by size in a line and pair the first with the last each time. The sum you get doing this is 18 for each of the pairs + 9.
I updated solution with possible cases with the logical steps.
i found the same result, using kind of the gauss theory, without even knowing it was his. i mean in the specific problem it was clear that you had to take as the center block, the biggest number as you want to maximize the sum. the step ahead was to find a way to make every couple of the other numbers equal with the other, so you just need to pair first and last of the remainng 8,and couple them. What i am trying to say is that i think the specific problem is more of a logical than a mathematical
The sequence of digits given in the problem is an arithmetic progression and in an A.P sum of terms equi-distant from beginning and end is constant.
The answer is 1 8 but I did it by trial and error. I placed the numbers in the boxes until I got the maximum sum.
There's a quick way to show it's the maximum. Think about the sum of these numbers.
I just placed the larger number in the center square.
If I am looking for the largest value and I must use all numbers then I start with the smallest value. Which is 1. So what is the largest value I can achieve if 1 is one of the numbers. That is 1+8+9=18. No larger sum can be achieved. Placing 9 in the center with 1 on one side and 8 on the other. It becomes easy to fill in the remaining boxes to add each to 18.
I thought you always put the highest in the middle. The next number (8) is offset by (1) so on and so forth, no advanced math needed for this one
We can start by writing sum of all digits i.e 45.
If we assign variables a,b,c,d,e,f,g,h,i. Putting e at the centre box.
As condition is the sum along the lines is same but actually the centre box doesn't bothers the sum, i.e the sum of boxes other than the central box is also the same.
a+b+c+d+e+f+g+h+i= 45
a+i=b+h=d+f= g+c=∆-e (∆=sum along lines)
4(a+i)+e=45. So 4(∆-e)+e=45
4∆-3e=45. So. ∆=45+3e\4
So ∆is max. When e is max. But ∆ is integer only when e=5,9
But we want max. So e=9. So ∆= [18]
L e t t h e h i g h e s t n u m b e r g o i n t h e m i d d l e a n d t h e h i g h e s t s u m t h a t c a n b e f o r m e d b e t w e e n t w o n u m b e r s f o r a l l t h e r e m a i n i n g n u m b e r s g o i n t h e i r r e s p e c t i v e p l a c e s ,
9 i s t h e h i g h e s t n u m b e r a n d t h e h i g h e s t n u m b e r t h a t c a n b e f o r m e d f r o m t h e r e m a i n i n g n u m b e r s .
H e n c e , 9 + 9 = 1 8
T h e r e f o r e , t h e m a x i m u m p o s s i b l e s u m t h a t c a n b e a c h i e v e d i s 1 8 .
to maximise each line I needed to put the max number possible in the middle box which is : 9 and then I tought that every two boxes must have same outcome, and instinctly got 9 8+1 7+2 6+3 5+4
To maximize our value - We put 9 in the middle, then we have 1-8 notice that pairing off gives us 1+8 2+7 3+6 4+5 this is 9 for all pairs, then putting this on our line we get 18 as our sum.
How do you know that "To maximize our value - We put 9 in the middle"?
I know this because the 9 will go to all pairs, and therefore increasing the value.
Every line shares the central, so for all lines to add up to the same value the outer numbers of every line also have to add up to the same value.
Chosen any central number the biggest of the remaining numbers has to be matched with the smallest, otherwise, the smallest number should be matched with a number bigger than the biggest in order for the pair to have the required sum.
We can, therefore, say that the sum of any line is equal to the sum of the central number and the biggest and smallest of the remaining. The number 9 will always be either the central one or the biggest one. Similarly, the number 1 will always be either the central one or the smallest one. Therefore 9 and 1 will always be in the same line.
We can choose the last number of the line however we want and therefore to maximize the sum we choose 8. So the result is 9 + 8 + 1 = 1 8
I find that hard to follow, but ultimately understood your third paragraph.
At the end, you only explain why the maximium cannot be more than 18. We still have to show that 18 can work.
For each sum of numbers in a line to be a maximum each must contain the number 9, Hence place 9 in the middle.
Now for the surrounding numbers realize that for all numbers in a line to sum to the same each number startng with 1 must be paired with the largest number yet unused.
Hence the pairs (1,8) , (2,7), (3,6) , (4,5)
Why is the first line true?
1+2+3+........+9 = 45
as per magic box total is equal to 60.......[45 + 3 * 5 = 60
now by considering 9 instead of 5 total becomes.....45 + 3 * 9 = 72
72/4 = 18
What do you mean by "by considering 9 instead of 5"?
Means replace digit 5 with 9,
Note; if we replace digit 5 with 6 or 7 or 8 we do not get ans. in hole no. only it is possible with 9
There are four lines in the diagram, each producing the sum S . Adding these four sums together, we add together the numbers in all nine boxes, but the middle number m is counted four times. Thus: 4 S = 4 m + ∑ other boxes 4 S = 3 m + ∑ all boxes 4 S = 3 m + ∑ numbers from 1 to 9 4 S = 3 m + 4 5 .
Therefore the sum is greatest if m is greatest. Also, because S is an integer, 3 m + 4 5 must be a multiple of four. This is only possible if m is one more than a multiple of four; in other words, m = 1 , 5 , 9 .
It makes sense first to try m = 9 . This means S = 1 8 , so that the numbers not in the middle should add up to 9 in pairs. It is easy to do this: 9 = 1 + 8 = 2 + 7 = 3 + 6 = 4 + 5 . Thus we place 1 across from 8, 2 across from 7, and so on. It does not matter where! This proves that the maximum sum is 1 8 , and that this can actually be done.