Almost a Pythagorean Triple

Number Theory Level 4

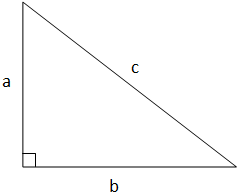
You're given a right triangle as shown above. If a a is a positive integer such that it satisfies the constraints a ∣ c a|c and b 2 = a ! + ( a − 1 ) ! + ( a − 2 ) ! b^{2} = a! + (a-1)! + (a-2)! , what is the largest known value of a a ?

Hint : The related problem remains one of the world's unsolved math mysteries.


The answer is 9.

Worranat Pakornrat by Worranat Pakornrat , 36, Thailand

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

From the Pythagorean theorem, a 2 a^{2} + b 2 b^{2} = c 2 c^{2} .

Then b 2 = a ! + ( a − 1 ) ! + ( a − 2 ) ! = [ ( a − 2 ) ! ] ( a ( a − 1 ) + ( a − 1 ) + 1 ) = [ ( a − 2 ) ! ] ( a 2 b^{2} = a! + (a-1)! + (a-2)! = [(a-2)!](a(a-1) + (a-1) +1) = [(a-2)!](a^{2} ).

Thus, a 2 a^{2} + b 2 b^{2} = a 2 a^{2} + [ a − 2 ) ! ] ( a 2 a-2)!](a^{2} ) = c 2 c^{2}

Since a ∣ c a|c , c 2 c^{2} = a 2 a^{2} d 2 d^{2} for some integer d.

Dividing a 2 a^{2} both sides, we will get: 1 + ( a − 2 ) ! (a-2)! = d 2 d^{2} .

This equation leads to the famous Brocard's problem: find the natural number n such that n!+1 is a perfect square.

Until now, there are only 3 known values for n: 4, 5, and 7.

4! + 1 = 25 = 5^2.

5! + 1 = 121 = 11^2.

7! + 1 = 5041 = 71^2.

By checking up to a billion, no other larger integers satisfy the condition, and many believe 7 is the highest number despite having no standard proofs yet.

As a result, since a − 2 a-2 = 7, the maximum known value of a a is 9.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...