Almost a soccer ball
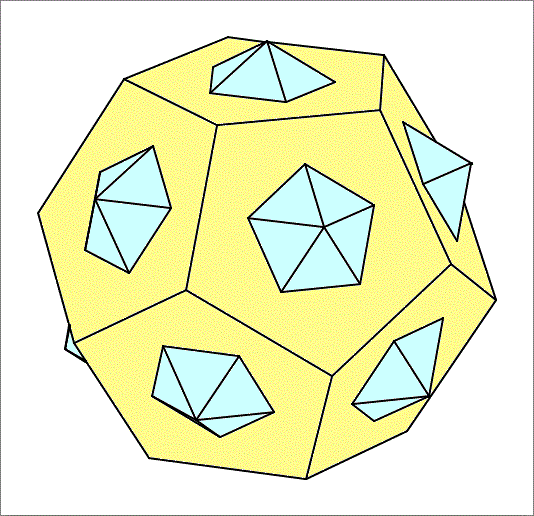
A dodecahedron and an icosahedron intersect as shown above. Their edge lengths are such that the intersection (i.e. taking the points that are inside the dodecahedron and inside the icosahedron) results in the polyhedron shown below, where all faces are regular pentagons and hexagons of side length . Find the volume of this polyhedron which is almost like a soccer ball.
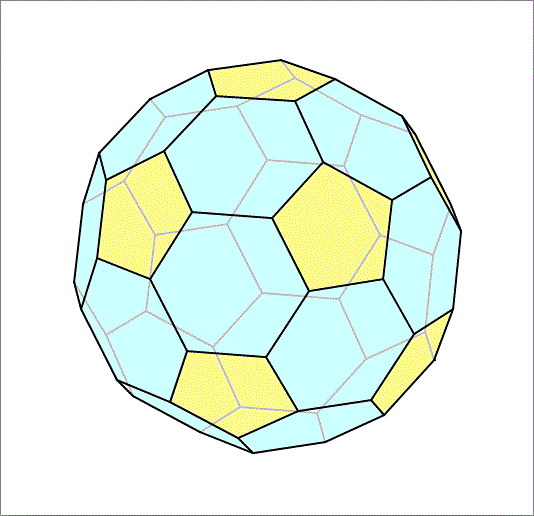
The answer is 55.2877.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I used the shortcut of looking up the formula of icosahedron, and from the question deduced that the original one before the trimming is size 3. Then I just deducted the volume of 12 pentamids from the results.
Formula for volume of icosahedron
= 5(3 + √5)s³ / 12.
V_icos(3) = (135 + 45√5) / 4.
Volume of a unit of icosahedral vertices' uniform pentamid of size 1.
= (5 + √5) / 24.
Football-ey Volume.
= V_icos(3) - 12 x [(5 + √5) / 24].
= (125 + 43√5) /4