Almost A Sphere, But Not Quite
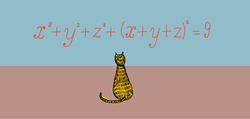Let
x
,
y
,
z
be real numbers such that
x
2
+
y
2
+
z
2
+
(
x
+
y
+
z
)
2
=
9
and
x
y
z
≤
3
2
1
5
. To 2 decimal places, what is the greatest possible value of
x
?
The answer is 2.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Discussions for this problem are now closed
The first condition is equivalent to x 2 + ( y + z ) 2 + ( x + y + z ) 2 = 9 + 2 y z . Let y + z = u , then we get that
x 2 + u 2 + ( x + u ) 2 = 9 + 2 y z ⇒ 2 ( x 2 + x u + u 2 ) = 9 + 2 y z ≤ 9 + 1 6 x 1 5
Since 2 ( x 2 + x u + u 2 ) = 2 ( 4 3 x 2 + ( u + 2 1 x ) 2 ) ≥ 2 3 x 2 , hence we have the inequality
2 3 x 2 ≤ 9 + 1 6 x 1 5 ⇒ 8 x 3 − 4 8 x − 5 ≤ 0
The cubic has roots 2 5 > 4 1 ( 2 1 − 5 ) > − 4 1 ( 2 1 + 5 ) , and so the largest value of x is 2 . 5 .
It remains to show that this can be achieved. From above, we need equality and so ( x + 2 u ) 2 = 0 and x y z = 1 6 1 5 , which gives us y + z = u = − 2 x = − 4 5 and y z = 1 6 x 1 5 = 1 6 3 . We can solve this (vieta + quadratic equation) to get that { y , z } = { 8 1 3 − 5 , 8 − 1 3 − 5 } . Hence, the maximum value is x = 2 5 .
Where did the 3/2*(x^2) come from?
By the trivial inequality, ( u + 2 1 x ) 2 ≥ 0 , hence, the expression is greater than or equal to 2 × 4 3 x 2 = 2 3 x 2 .
From the first condition, we can assume z = 0 . Also, this makes the 2 nd condition naturally true. Then we're left with x 2 + y 2 + ( x + y ) 2 = 9 ⟹ 0 = x 2 + x y + y 2 − 2 9 . Using the quadratic formula, it suffices to maximize x = 2 − y ± 1 8 − 3 y 2 . This is not hard to maximize to get 6 using the method of your choice (mine was very messy calculus due to time's sake). Question to the reader: what method would you use? :D
Moderator note:
This solution is wrong, and it makes the invalid assumption that z = 0 . The answer is not 6 , but 2.5 instead.
Why can we assume that z = 0 ?
Note that the answer is not 6 , but actually 2.5. The equality condition occurs at x = 2 5 , y = 8 1 3 − 5 , z = 8 − 1 3 − 5 ,
Calvin Lin can u present the solution of this problem?
i could answer that EQUTAION
srry i dint get u!
This is my friend 's solution. from the first condition we have 2xy=x^2+(y+z)^2+(x+y+z)^2-9. replace x+y=t the equation becomes 2xy=x^2+t^2+(t+x)^2-9 <==>2(x^2+t^2+tx)-9=2xy<==>2xy=2(t+x/2)^2+3x^2/2-9>=3x^2/2-9 Case 1: With x>=sprt(6)==> 2xy>=0 using second condition: 15/32>=xyz>=1/2*x(3x^2/2-9) ==>3x^3/4-9/2x-15/32<=0==>x<=5/2 So maximum possible value of x is 5/2. then find the value of y and z Case2: With x<sprt(6)<5/2 ==> maximum possible value of x is 5/2.
i made the use of second inequality. since xyz<15/32. and all of them are real no. we can write xyz<(3*5/2^5). the question asked for maximum value of x so it will be (5/2)=2.5
Your solution is not close, u don't use first condition
using A.M>G.M we get 15\32 > (X+Y+Z)^3\27 and another equation is given,on simplifying that we gat (x+y)^2 +(y+z)^2 +(x+z)^2 =9
Note that AM-GM is less likely to be applicable to this question, because the equality case is not when all the variables are equal.
In your inequality, you got the sign mixed around. The GM is 15/32.
I tried to use thee Laplace equation for this but came up a bit short at 2.05 must have made a miscalculation, I also presumed that x would be a max if x=z=y is this correct?
Note that for inequalities, the maximum / minimum need not necessarily occur when x = y = z .
Furthermore, when you want to find the maximum possible value of x , you often want to use different values of y and z . For example, what is the maximum value of x subject to x 2 + y 2 = 1 ?
how can i join pharmacy related subjects
Set t = y z and u = y + z After plugging in and some computation, we get 2 x 2 + 2 x u + 2 u 2 = 9 + 2 t . Now using the second condition, 1 6 x 1 5 + 9 ≥ 2 x 2 + 2 x u + 2 u 2 . Simplifying, 2 x 3 + 2 x 2 u − 9 x − 1 6 1 5 + 2 u 2 x ≤ 0 . For the maximum possible x to still satisfy the equation, u must be such that the left side is as small as possible. Thus we can find by taking the derivative with respect to u that x is maximized when x = − 2 u , and plug back in to get a cubic which has the solution x = 2 5
Note: the fact that we must have u 2 ≥ 4 t could have created some problems, but in this case it didn't.