Almost A Square, But Not Quite
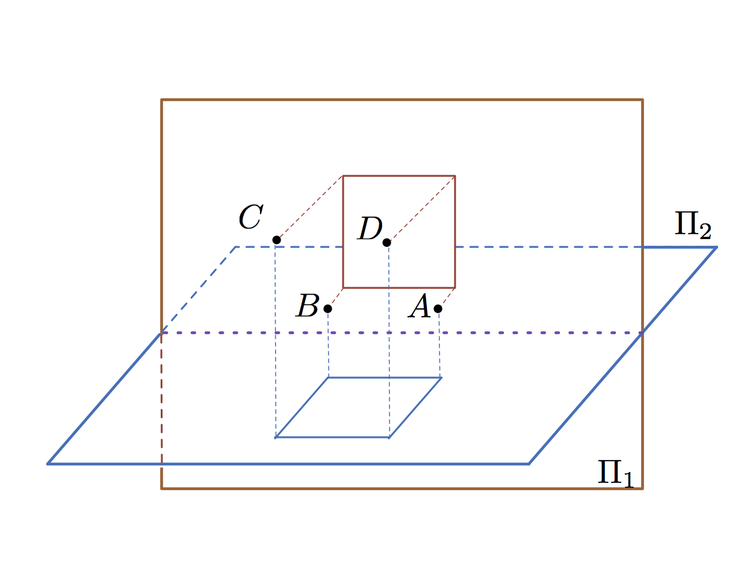 Suppose
A
,
B
,
C
and
D
are 4 points in space that lie on the same plane, with
A
B
C
D
being a quadrilateral. There are 2 perpendicular planes
Π
1
and
Π
2
, such that the orthogonal projections of
A
B
C
D
onto these planes form a square of area
1
2
3
each. If
∣
A
B
∣
=
1
2
,
what is the perimeter of
A
B
C
D
to 1 decimal place?
Suppose
A
,
B
,
C
and
D
are 4 points in space that lie on the same plane, with
A
B
C
D
being a quadrilateral. There are 2 perpendicular planes
Π
1
and
Π
2
, such that the orthogonal projections of
A
B
C
D
onto these planes form a square of area
1
2
3
each. If
∣
A
B
∣
=
1
2
,
what is the perimeter of
A
B
C
D
to 1 decimal place?
The answer is 54.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Same, but I didn't even bother with the exact junk. I just split it up into little 2-dimensional parts and solved. :P
Same method, nice soluttion @Patrick Corn
I did the same :)
first AB=(123)^0.5 ; AD=AB/ SIN 45 = (246)^0.5 ; when AB = 12 it is >(123)^0.5 ; so let denote new AB WITH A1B1 ; in traingle A A1 D ; AA1=[ 12-(123)^0.5 ]/2 ; A1D = [AD^2 + AA1^2 ]^0.5 =15.69 ; SO perimeter = 12+ 2* 15.69 +(123)^0.5 =54.47
 Imgur
I too got the same answer first (approx 54), by dividing the projected area = 123 sqrt(2) by 12. But then thought it may not be correct for the following -
Imgur
I too got the same answer first (approx 54), by dividing the projected area = 123 sqrt(2) by 12. But then thought it may not be correct for the following -
To get the side AB = 12 for ABCD (which has to be a parallelogram), the projections A1B1 and A2B2 of AB on the two planes, cannot be parallel to the line of intersection (the 'fold line') of the two planes. Because that would make ABCD a rectangle with two of the sides equal to sqrt(123) and other two sqrt(2) times that.
So let theta = angle made by one side of the square with the 'fold line'. and
L = side of the squares = sqrt(123).Then 1 2 = L 2 cos 2 θ + L 2 sin 2 θ + L 2 sin 2 θ θ = sin − 1 1 2 3 1 4 4 − 1 = 2 4 . 4 If phi = 90 - theta, then the other sides (AD & BC) of the parallelogram ABCD would be A D = L 2 cos 2 ϕ + L 2 sin 2 ϕ + L 2 sin 2 ϕ = 1 5 Giving the perimeter = 2(12+15) = 54
So the perimeter is exactly and not approximately 54 as I initially thought.
I put coordinates on everything: wlog A = ( 0 , 0 , 0 ) and the planes are x = 0 and y = 0 . If B = ( b 1 , b 2 , b 3 ) , then b 2 2 + b 3 2 = 1 2 3 , b 1 2 + b 3 2 = 1 2 3 , and b 1 2 + b 2 2 + b 3 2 = 1 4 4 . So b 1 2 = b 2 2 = 2 1 and b 3 2 = 1 0 2 . After some reflections, we can assume that B = ( 2 1 , 2 1 , 1 0 2 ) .
Proceeding similarly (and using reflections to choose signs wlog), we can get D = ( − 1 0 2 , − 1 0 2 , 2 1 ) and C = ( 2 1 − 1 0 2 , 2 1 − 1 0 2 , 2 1 + 1 0 2 ) . Then A B = C D = 1 2 and B C = A D = 1 5 , so the sum is 5 4 .
I'm sure there is a much nicer solution...?