Almost AIME
( 5 + 1 ) ( 4 5 + 1 ) ( 8 5 + 1 ) ( 1 6 5 + 1 ) 4
If the above expression is equal to x , find the value of ( x + 1 ) 6 4 .
The answer is 625.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
This is the best solution
can you do the bottom part with more steps, i meab how does that equal to 4
Log in to reply
Four applications of difference of squares.
i kinda dont understand how did you get the denominator "4" with its prev expression :(
Log in to reply
Consecutively multiplying from right to left, because ( 2 n 5 + 1 ) ( 2 n 5 − 1 ) = n 5 − 1
well done - once I figured out the math in the denominator!
Skips way too many steps just to get to the first statement
Nice problem.
Best usage of conjugates trick I've ever seen
Brilliant!
Yeah me too
Good usage of conjugate and identites
Wow ..too good bro
If you put some effort into doing the computation required, you will see why the missing steps are trivial, almost superfluous
To explain the second step, remember that ( a + b ) ( a − b ) = a 2 − b 2 , so the last two binomials become ( 1 6 5 ) 2 − 1 2 = 8 5 − 1 . The same rule can be applied to the next binomial, and then to the next until we are left with ( 5 + 1 ) ( 5 − 1 ) = ( 5 ) 2 − 1 2 = 5 − 1 = 4 . And with relative ease, the denominator simplifies to 4.
Elegance and beauty of mathematics....
I'm afraid my solution isn't as elegant as Alan Yan's, but still, her it is:
but it is a good try, be happy and there is always room for important
By far, the superior solution. Remembering the formula for the sum of this series is helps. Nice job Kris. Thanks.
What is the formula for the sum of this series in full?
It is good to see an alternate path, but it requires some thought to agree that all the coefficients are one for multiplying out D.
i thought mine was the only method but there are others(although basically same)................ write 4 = 5 − 1 then use identity a 2 − b 2 = ( a + b ) ( a − b ) , i would call it simple and elegant too.... ⌣ ¨
Good problem bro! :+1:

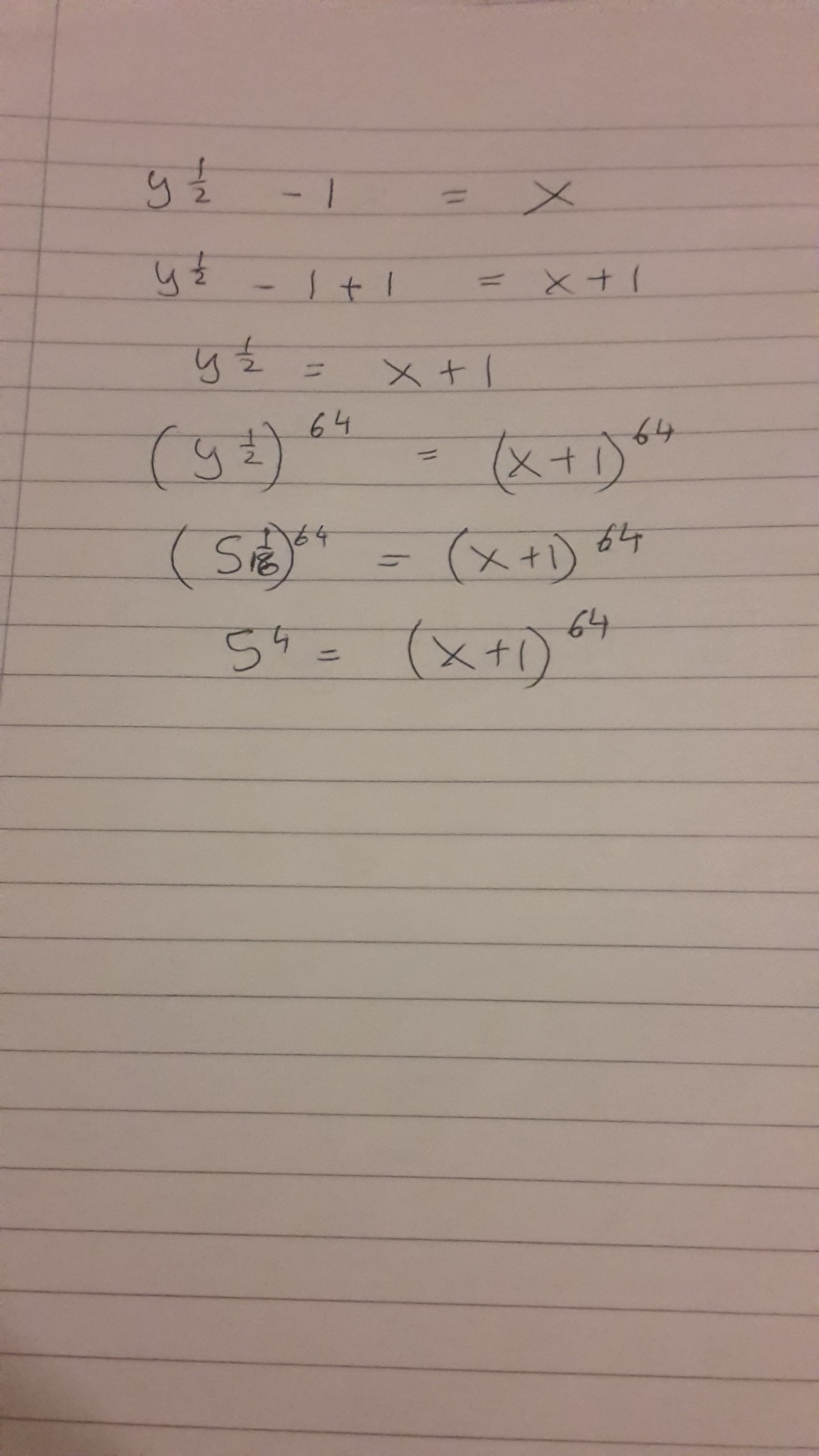
Pretty straightforward.
x = ( 5 + 1 ) ( 4 5 + 1 ) ( 8 5 + 1 ) ( 1 6 5 + 1 ) ( 1 6 5 − 1 ) 4 ( 1 6 5 − 1 ) = 4 4 ( 1 6 5 − 1 ) = 1 6 5 − 1 x + 1 = 1 6 5 ⟹ ( x + 1 ) 6 4 = 5 4 = 6 2 5