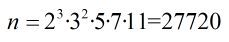Almost divisible by all 3

Use the Fundamental Theorem of Arithmetic. We guess the largest quality factor of n is 11 or 13,then we try to find the largest n. 1°when the largest quality factor is 13 We can easily find this condition is not satisfied 2°when the largest quanlity factor is 11

First, find the lcm of {1,2,3,...,n-1}, denoted by lcm([n]). Compare these with $n^4$ The last jump is at n = 13.

n = 13 => lcm([13]) = 27720 and $n^4$ = 28561.

n = 14 => lcm([14]) = 360360 and $n^4$ = 38416.

And this is clear that lcm([n]) grows faster than $n^4$ , so we don't have to test out all n.

Next, find the largest multiple of lcm[n] such that it is still less than $n^4$ .

Consider numbers from $n=12^4+1 = 20737$ up to $n=13^4 = 28561$ . These (and all numbers greater) need to be divisible by all numbers less than 13, or 1 through 12, in order to satisfy the property. The smallest number that satisfies this, lcm(1...12), is 27720. 27720 is a good number, since its fourth root is less than 13, and it's divisible by 1-12. Any number in the range must be a multiple of 27720 in order to satisfy, but 27720 is the only multiple of itself within the range.

Numbers from 28561+1 through 38416 need only be divisible by 1-13 to suffice, since 38416 has fourth root 14, and those numbers have fourth roots in (13,14], and so 'all integers smaller than the root' are 1-13, but the lcm of those is 360360. Clearly then no numbers from 28562 through 360359 can satisfy the property.

Here begins a process of runaway, as the necessary lcm grows at a greater rate than the fourth power. Before 360360 is reached, $16^4+1=65537+1$ has fourth root >16, and so any number from this onwards needs to be divisible by 1...16, the lcm of which is 720720. Beyond $17^4+1 = 83522$ , we require a multiple of 12252240, which is more than 146 times greater than 83522, a factor rapidly growing from the $360360/38416\approx 9$ seen earlier.

This is predicted by the density of primes. By Bertrand's postulate , a prime always exists between m and 2m for any m>1. The product of those primes then grows at least as fast as 1*2*4*8...*m. Alternatively, considering multiplication as logarithmic addition, in searching from some number m to 2m, we gain another term of $\log(m)$ onto the logarithm of the product, and taking the logarithm to be base 2, the sum appears like $\log(1)+\log(2)+...+\log(m/2)+\log(m) \approx 0+1+...+\log(m)-1+\log(m) \approx \log(m)^2$ . As m grows, the product of all primes <m grows like $2^{\log(m)^2}$ , which is a lower bound for the lcm of all natural numbers <m, which lower bounds any integer $n$ that is divisible by all numbers less than m. However, the logarithm of the fourth power of m is merely $\log(m^4) = 4\log(m)$ , so $m^4$ grows like $2^{4\log(m)}$ , which can compared directly as less than $2^{\log(m)^2}$ for sufficiently large m, and makes it impossible to find a satisfying $n$ , a multiple of the lcm, within $m^4$ and $(m+1)^4$ , or rather before another prime is introduced and the lcm grows again. This is a sketchy non-proof explanation of the phenomenon, but I hope it aids in understanding.

Python code to find the answer:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

from functools import reduce
def gcd(a, b):
    while b:      
        a, b = b, a % b
    return a

def lcm(a, b):
    return a * b // gcd(a, b)

i = 1
while True:
  i = i+1
  x = reduce(lcm,range(1, i))
  if i**(4) < x:
    break
print (i)

You can try it here

Just use some code here:

#include <iostream>
#include <cmath>
using namespace std;
int main(){
    int flag, max = 0;
    for(int n = 2; n < 100000; ++n){
        flag = 1;
        for (int j = 2; j < sqrt(sqrt(n)) && flag; ++j)
            if(n % j != 0)
                flag = 0;
        if(flag)
            max = n;
    }
    cout << max;
}