Almost Magic
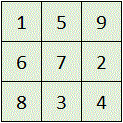How many different ways can the digits
through
be placed in a
grid so that all the rows and columns (but not necessarily diagonals) add up to the same number?
The answer is 72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are nine places for the '1'. The other two squares in both the row and column of the '1' must add to 14, and the only way to do that is to select '5' and '9' for one set and '6' '8' for the other. Thus there are 4 squares to place the '5', and placing the '5' forces the placement of the '9. That leaves 2 spaces for the '6', and that forces the placement of the '8'.
Once those five digits are placed, the last four positions are forced. The '7' cannot be in the row or column of either the '8' or '9', so it must be placed where the '5' row/column crosses the '6' column/row (as in the picture). Placing the '7' forces the placement of the '3' and '2', leaving the last square for the '4'.
Recapping 9 (choices for the '1') x 4 (choices for the '5') x 2 (choices for the '6') = 72 possibilities.