Almost Primes Square

Algebra Level 5

You're given a 4 × 4 4\times 4 magic square, where the sum of every row, column, or diagonal equals to 180, and all the letters A A to O O represent distinct 2-digit prime numbers apart from 49 as shown.

The unit numbers never repeat in any sum, and the corner numbers are arranged such that the product A O L C AOLC is maximum.

If A A > O O > L L > C C , what is the value of A A + B B - C C + D D - E E + F F - G G + H H - I I + J J - K K + L L - M M + N N - O O ?


The answer is 45.

Worranat Pakornrat by Worranat Pakornrat , 36, Thailand

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

If we add the sums of the two diagonals and four edges together, we will get:

6 × 180 6\times 180 = 3( A A + C C + L L + O O ) + ( B B + D D + E E + F F + G G + H H + I I + J J + K K + M M + N N )

Subtracting the sum of four rows (A to O) from the sums above, we will get:

( 6 − 4 ) × 180 (6-4)\times 180 = 360 = 2( A A + C C + L L + O O )

Thus, 180 = A A + C C + L L + O O .

That means the sum of the corner numbers also equals to 180, and from comparing the sum of corner numbers and the diagonals, we will get:

A A + C C + L L + O O = A A + E E + J J + O O = C C + F F + I I + L L

C C + L L = E E + J J and A A + O O = F F + I I

Therefore, A A + C C + L L + O O = E E + F F + I I + J J = 180.

That means, not only the corner numbers add up to 180, but also the central ones!

Also, C C - E E = J J - L L and A A - F F = I I - O O , restricting the gaps along the knight-move orders.

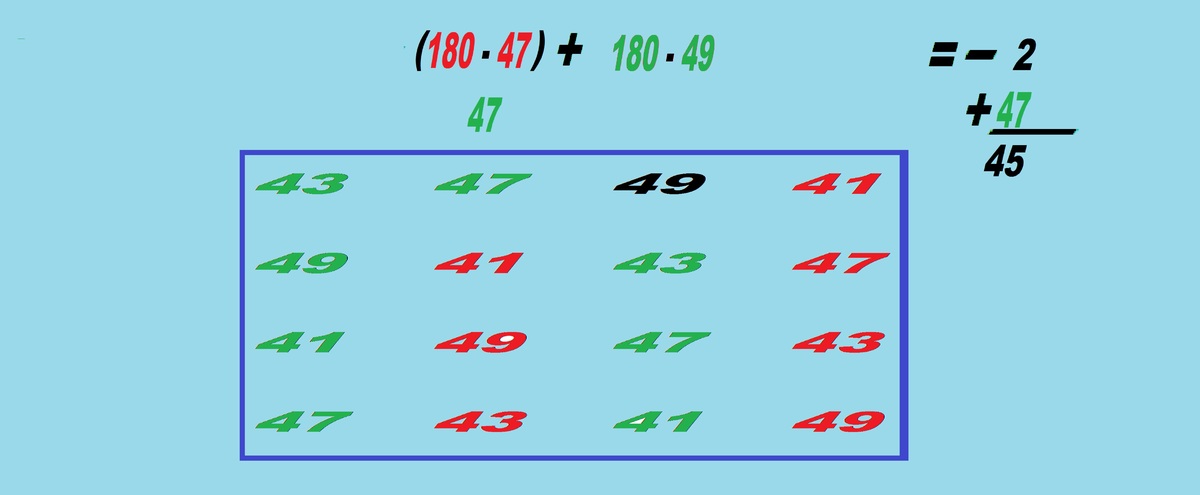
Since all the alphabetical variables are all primes, to get equal amount in each row, column, or diagonal, the ending digits 1, 3, 7, 9 should be spread equally among the squares. Here is one example:

...1 ...7 49 ...3 ...9 ...3 ...1 ...7 ...3 ...9 ...7 ...1 ...7 ...1 ...3 ...9

With one known number 49, all we need to do is to plug in the digits that fit the restrictions above, and we know that the sum of the 4 digits will equal to 16 because 180 - (1+3+7+9) = 160.

With trial & error, we will reach a conclusion that the gaps between the corner and central numbers will equal to 2, and the solution magic square is shown below:

As a result, A A + B B - C C + D D - E E + F F - G G + H H - I I + J J - K K + L L - M M + N N - O O = 61 +47 - 23 + 29 - 43 + 41 - 67 + 53 - 79 + 17 - 31 + 37 - 11 + 73 - 59 = 45.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Very sorry my answer does not have distinct prime as required. \color{#D61F06}{\text{Very sorry my answer does not have distinct prime as required.}}

The missing total in the 1st column is 180 − 49 = 131. 131 3 = 43 2 3 . / t e x t P r i m e n e a r 43 a r e 41 , 43 , 47 , a n d 41 + 43 + 47 = 131. So using these numbers and 49 so that no number appears twice in any row , column or diagonal, we get the above square. 180 - 49 = 131.~~ \dfrac {131} 3 =43\frac 2 3.\\ /text{Prime near 43 are 41 , 43 , 47 , and 41 + 43 + 47 =131.} \\ \text {So using these numbers and 49 so that no number appears twice in any}\\ \text{row , column or diagonal, we get the above square.}\\~~\\

1st column is plus. Last minus. They add up to zero.
Second column 180 minus 47 =133 is minus.
That 47 plus third column less 49=47+180-49=180-2=178 is plus.
So required sum is 178 - 133= 45 \Huge ~~~~~~~~~\color{#D61F06}{45}


0 Helpful 0 Interesting 0 Brilliant 0 Confused

Actually there's way you can use distinct primes for this magic square (no repeated numbers) though you've got the right answer. ;)

Worranat Pakornrat - 5 years, 5 months ago

Log in to reply

Sorry, I again missed the point. You are right. The way I got the total may be easier.

Niranjan Khanderia - 5 years, 5 months ago

1 pending report

Vote up reports you agree with

×

Problem Loading...

Note Loading...

Set Loading...