Alpha and Beta
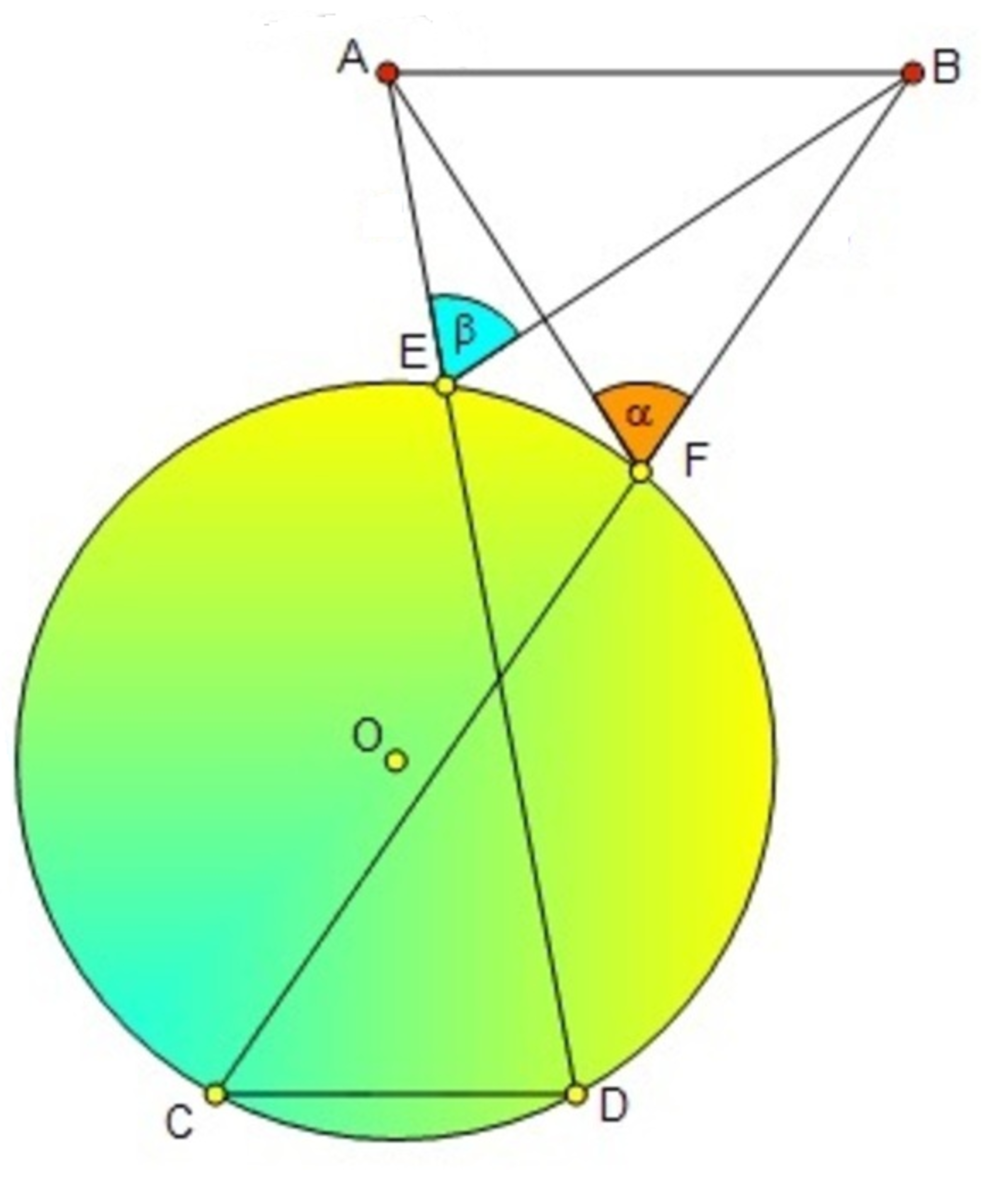
Two chords C F and D E of a circle centered at O are extended to B and A respectively such that A B is parallel to C D . Find the relation between α and β .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
But then the points A , B , F , E are concyclic, which implies ∣ C I ∣ = ∣ D I ∣ for all the positions of the point I . How is it possible? Am I making a mistake?
Log in to reply
Yes, points A , B , F , E are concyclic, but why does this imply that ∣ C I ∣ = ∣ D I ∣ ?
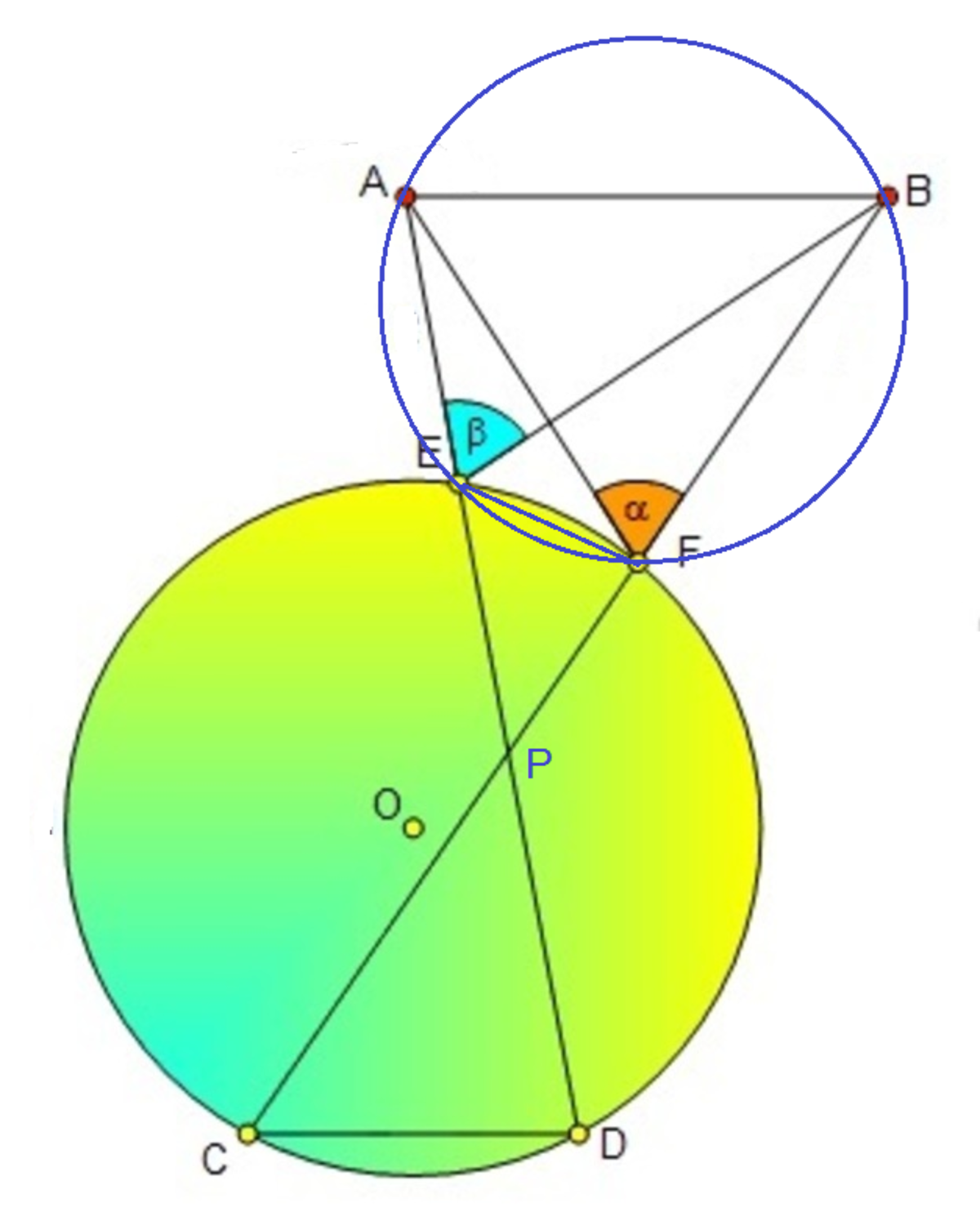
Let A D and B C meet at P . Since A B is parallel to C D , △ A B P and △ C D P are similar. Also C D F E is a cyclic quadrilateral , △ E F P is also similar to the other two triangles. This means that ∠ E F P = ∠ E A B and opposite angles ∠ E A B + ∠ B F E = 1 8 0 ∘ . Therefore A B F E is a cyclic quadrilateral and α = β .
maybe a little stupid, but nevertheless... construct EF. so angles DEF=DCF and EFC=FCD because they are inside angles of circle. FCD=ABF and CDE=EAB because of parallel AB and CD. DEF=ABF and AEF=180-DEF=180-ABF, so ABEF can be inscribed. If ABFE is inscribed - AEB=AFB inscribed angles to same horde.
Let the intersection point of A D and B C be point I , from intersecting chords theorem in a circle we know that E I ⋅ D I = C I ⋅ F I , and from the fact that △ I C D and △ I B A are similar it follows that D I C I = A I B I , hence D I C I = F I E I = A I B I ; this combined with the fact that the angle between E I and B I is the same angle between F I and A I , implies that △ A F I is similar to △ B E I . Thus ∠ A F I = ∠ B E I , hence α = β .