Already completely empty
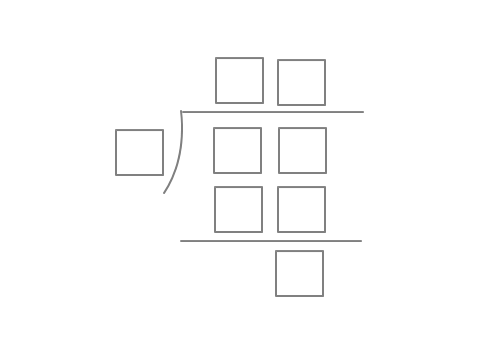 The above shows a condense form of a long division between 2 integers, with the last box at the bottom representing the remainder of the quotient. Each box represents a
distinct
single digit non-negative integer.
The above shows a condense form of a long division between 2 integers, with the last box at the bottom representing the remainder of the quotient. Each box represents a
distinct
single digit non-negative integer.
If 8 digits must be used, what is the largest possible integer that can represent the box at the very bottom?
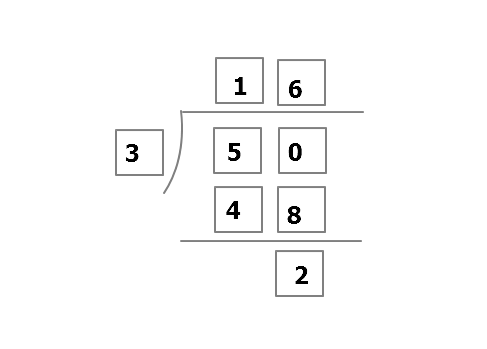
As an explicit example, the long division below shows that 2 is a possible remainder, but it does not imply that 2 is a maximum possible remainder.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since we are dividing by a single digit integer, our maximum remainder can be 8
So let us analyse whether we can achieve remainder of 8 or not
Case 1: Remainder of 8
We have to divide by 9 to achieve a remainder = 8
The sequence of numbers 1 7 , 2 6 , 3 5 , 4 4 , 5 3 , 6 2 , 7 1 , 8 0 , 8 9 , 9 8 produces remainder = 8 when divided by 9
We notice that in this sequence upto 8 0 , if a b is divided by 9 then we need to multiply 9 by a which is a repetition of digit a and not allowed.
Now 8 9 and 9 8 both contain 8 in them and reimainder is also 8 but this contradicts that all digits written in long division must be distinct.
So a remainder of 8 is not possible .
Case 2: Remainder of 7
First we try to divide by 9
The sequence of numbers 1 6 , 2 5 , 3 4 , 4 3 , 5 2 , 6 1 , 7 0 , 7 9 , 8 8 , 9 7 produces a remainder of 7 on division by 9
We remove 7 0 , 7 9 , 8 8 , 9 7 from our list as 7 cannot both be in the number and the remainder and in 8 8 we have already 8 repeated two times.
Upto 6 1 by the same previous logic we need to multiply 9 by the first digit of that number, example, 6 1 = 9 × 6 + 7 Here 6 is repreated and hence is not accordance with the rules
Now we check that can we get remainder of 7 when we divide by 8
Here the required sequence is 1 5 , 2 3 , 3 1 , 3 9 , 4 7 , 5 5 , 6 3 , 7 1 , 7 9 , 8 7 , 9 5
we remove 4 7 , 7 1 , 7 9 , 8 7 because they contain 7 and remainder is also 7 .This repeats 7 and is not allowed. 5 5 is also removed as it has 5 two times.
8 × 7 + 7 = 6 3 is also removed because we divide by 7 and remainder is also 7 which is not allowed.
We are left with 1 5 , 2 3 , 3 1 , 3 9 , 9 5
Now for 1 5 , 2 3 , 3 1 we need to multiply 8 by their first digits which forces a repetition of 1 , 2 , 3 respectively. For 3 9 = 8 × 4 + 7 = 3 2 + 7 in which 3 is repeated. In case of 9 5 we need 8 to multiply by 1 1 so that 1 is repeated.
In this case also we cannot get a remainder of 7
Conclusion: Remainder of 7 is also not possible to achieve
Case 3: Remainder of 6
Remainder of 6 is achieved in this way
9 0 = 7 × 1 2 + 6 = 8 4 + 6
So the answer is 6 since we checked that no one of the greater remainders are possible.
NOTE: If I can write long division box like @Pi Han Goh then my solution will be better but I don'tknow how to write. Can anybody suggest how to make this long division box and write numbers in it.