Alright Tetrahedron
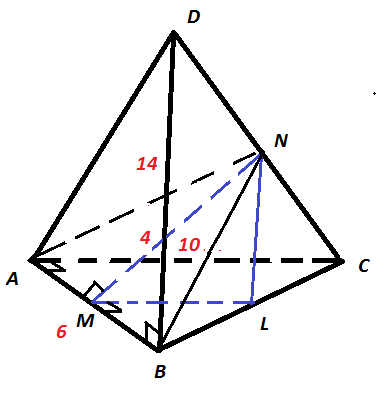
In a tetrahedron A B C D , the lengths of A B , A C , and B D are 6 , 1 0 , and 1 4 respectively. The distance between the midpoints M of A B and N of C D is 4 . The line A B is perpendicular to A C , B D , and M N . The volume of A B C D can be written as a b , where a and b are positive integers, and b is not divisible by the square of a prime number. What is the value of a + b ?
The answer is 38.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
We have that the volume of the tetrahedron N A B D is the half than the volume of the tetrahedron A B C D because the base A B D is in common and the height from N is half than the height from C because N D = 2 C D . The volume of the tetrahedron C A B N is equal to the volume of the tetrahedron N A B D that is half than the volume of A B C D . By considering the base A B C of the tetrahedron A B C N we have that the height from N falls on the axis of A B because M N is perpendicular to A B .
We call L the midpoint of B C and we have that the axis of A B meets B C in L because the triangle M B L is similar to the triangle A B C and the rate is 2 1 . Now we consider the triangle N M L and we suppose ∠ N M L = α . We have that N L = 7 because the triangle C N L is similar to the triangle C D B and the rate is 2 1 and M L = 5 for the same reason. So we have N L 2 = M N 2 + M L 2 − 2 M N ⋅ M L cos ( α ) for the cosine rule. So cos ( α ) = − 5 1 and sin ( α ) = 5 2 6 .
Now we have that the height from N to A B C is given by N M sin ( α ) and the area S of A B C is 3 0 ( A B and A C are catheti). So the volume of A B C N is given by 3 S ⋅ N M sin ( α ) and so the volume of A B C N is 1 6 6 . So the volume of the tetrahedron A B C D is 3 2 6 . So a = 3 2 and b = 6 and so a + b = 3 8 .
[Note: It is easier to calculate that [ M L N ] = 4 6 , so the volume of M L N B is 3 1 ⋅ ∣ M B ∣ ⋅ [ M L N ] = 4 6 , hence the volume of A B C N is 4 times that, which is 1 6 6 . - Calvin]
The hard part of 3-D geom is to make sense of the figure, and find enough information to piece it together. Stefano shows how we can deconstruct the tetrahedron and build our way up, while Erick shows how choosing suitable coordinates and reference frames simplifies the problem greatly.
The diagram matches Stefano's description.
Suppose L is the midpoint of B C . Then M L is parallel to A C , so perpendicular to A B . Because M N is perpendicular to A B , the plane M L N is perpendicular to A B . Note that the length of M L is half of the length of A C , so it is 5 . Similarly, the length of N L is 7 , the triangle M L N has side lengths 4 , 5 , and 7 .

Lemma. The area of the triangle M L N is 4 6 .
Proof of the Lemma. Suppose the measure of the angle M L N is α . From the Law of Cosines, cos α = 2 ⋅ 2 ⋅ 5 4 2 + 5 2 − 7 2 = − 5 1 . So sin α = 1 − cos 2 α = 5 2 4 . The area of M L N is 2 1 ⋅ 5 2 4 ⋅ 4 ⋅ 5 = 2 2 4 = 4 6 .
Because A B is perpendicular to M L N , the segment B M is the height of the tetrahedron M L N B , when viewed with the base M L N . So the volume of M L N B is 3 1 ⋅ 3 ⋅ 4 6 = 4 6 .
Consider the tetrahedra A B C N and M B L N . They have the same vertex N and their faces opposite to N lie in the same plane. Because the triangle A B C is similar to the triangle M B L with the proportionality coefficient 2 , the area of A B C is four time the area of M B L , so the volume of A B N C is 4 ⋅ 4 6 = 1 6 6 .
Finally, consider the tetrahedra A B C D and A B C N as having the same vertex A and opposite faces in the same plane. Clearly, the area of B C D is twice the area of B C N . So the volume of A B C D is 2 ⋅ 1 6 6 = 3 2 6 , and the answer is 3 2 + 6 = 3 8 .
I'm finding this question confusing. There is a right angle at ABD and BAC. This gives us our respective base and height. The base is the triangle at the bottom with an area of (6)(10)/2=30. The height is 14 from the right angle at ABD. So the volume is 30*14/3=140?????? That's not the correct answer, can someone show me why?
V = 3 1 ∗ A b ∗ H . A r e a Δ A B C = A b = 2 1 ∗ 6 ∗ 1 0 = 3 0 . L e t Δ A B C b e i n h o r i z o n t a l p l a n e . Δ N M L M N ⊥ A B , s o Δ N M L i s i n t h e v e r t i c a l p l a n e . L e t h b e t h e h e i g h t o f N a b o v e M L . M L = 2 1 ∗ A C = 5 . N L = 2 1 ∗ B D = 7 . N M = 4 . 2 1 ( 5 + 7 + 4 ) = 8 . 2 1 ∗ M L ∗ h = i t s a r e a b y H e r o ′ s . ⟹ 2 1 ∗ 5 ∗ h = 8 ∗ ( 8 − 5 ) ( 8 − 7 ) ( 8 − 4 ) = 4 ∗ 6 . h = 5 2 ∗ 4 ∗ 6 . B u t N i s t h e m i d p o i n t o f C D . V ⟹ H = 2 ∗ h = 5 1 6 ∗ 6 V = 3 1 ∗ 3 0 ∗ 5 1 6 ∗ 6 V = 3 2 ∗ 6 = a b . a + b = 3 8 Thank you, Clvin Lin, it is very clear diagram making the problem solution easy.
WLOG we assume A is at the origin, B is at (6,0,0) and C is at (0,10,0), so that the base ABC (of area 30) lies in the xy-plane. To get the volume of ABCD we just need the z-height of D. Clearly M is at (3,0,0), and if MN is orthogonal to AB we must have N = (3,x,y) for some x,y. Since N is the midpoint of CD this puts D at (6,2x-10,2y). Since ∣ M N ∣ = 4 we have x 2 + y 2 = 1 6 , while ∣ B D ∣ =14 gives us ( x − 5 ) 2 + y 2 = 4 9 . Subtracting these yields x = -4/5, and then y = 8√6/5. The height of D is therefore 2y=16√6/5, giving a volume of [ABCD] = 32√6.