Always moving away!
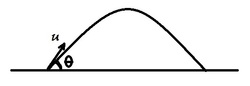 A projectile is launched at an angle
with initial velocity
. Let
be the largest acute angle for which the projectile is always moving away from its launch point. Determine
(in degrees).
A projectile is launched at an angle
with initial velocity
. Let
be the largest acute angle for which the projectile is always moving away from its launch point. Determine
(in degrees).
Details and Assumptions:
The answer is 70.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The square of distance X = x 2 from the point of projection as a function of time is given as :
X = u 2 cos 2 θ t 2 + ( u sin θ t − 2 1 g t 2 ) 2
Now, since x always increases, hence X always increases. Hence, d t d X ≥ 0
Hence, 2 u 2 cos 2 θ t + 2 ( u sin θ t − 2 1 g t 2 ) ( u sin θ − g t ) ≥ 0
Rearrange to get :
g 2 t 2 − 3 g u sin θ t + 2 u 2 ≥ 0
Now, the value of t at which above function attains minimum is 2 g 3 u sin θ which is in the interval of time of flight.
Hence, discriminant = 9 g 2 u 2 sin 2 θ − 8 u 2 g 2 ≤ 0 ⇒ sin θ ≤ 3 2 2 , corresponding to 7 0 . 5 ∘