A.M G.M?
In the domain ( 0 , π ) , what is the minimum value of
sin θ + sin θ 2 ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
man the minimum value is occuring at 45 degree that is simply 2(1.41)=2.82
Log in to reply
sorry...you r correct
Log in to reply
: sorry...you r correct sin theta cant be greater than 1
Can anyone tell me why. I use AM-GM only. Then i got sin θ + sin θ 2 ≥ 2 2 . So I think it's 2 . 8 2 .
Log in to reply
Is it possible that sin θ + sin θ 2 = 2 2 ?
Solving this equation, we eventually get sin θ = 2 , which is not possible.
@Raj Rajput @Calvin Lin I think Titu's lemma also works for this problem, since θ ∈ ( 0 , π ) , and thus sin θ > 0 . We have sin θ + sin θ 2 = 1 sin θ + sin θ 1 + sin θ 1 ⩾ 1 + sin θ ( sin θ + 1 ) 2 + sin θ 1 = sin θ + 1 + sin θ 1 Equality occurs when sin θ + sin θ 2 = sin θ + 1 + sin θ 1 ⟹ sin θ 1 = 1 ⟹ sin θ = 1 ⟹ θ = 2 π Therefore, the minimum value is sin 2 π + sin 2 π 2 = 3 .
There isn't a min value for a .
Let s i n ( x ) = − 1 , we then get − 3 .
But we get let it tend towards − ∞ .
Log in to reply
In A.M and G.M inequality the numbers are positive, but I should mention that sorry edited and sinx is not equal to zero too .... sorry
The last step is very doubtful. The best way to do this question is by plotting the graph.
"Equality holds true when all the terms are equal" Equality or Inequality? And all the terms are equal? How do you figure?
I think that the title of this question was little bit misleading becase this question could be done by simple algebraic manipulation.
Y= Sin X+2/(Sin X)=Sin X (Sin X × Sin X +2)
As we know that Sin value can be maximum 1 , therefore y(max)=3.
0 < θ < π
0 < sin θ ≤ 1
sin θ + sin θ 2
= ( sin θ + sin θ 1 ) + sin θ 1
When sin θ = 1 ,
sin θ + sin θ 1 has minimum value 2 and sin θ 1 has minimum value 1 at the same time.
So the minimum value of sin θ + sin θ 2 is 2 + 1 = 3
It should be when sin x is a positive real no., for all the real values of x, this equation has min. value of -(infinity). thus , the correct option should be none of these..... would be much easier then :)
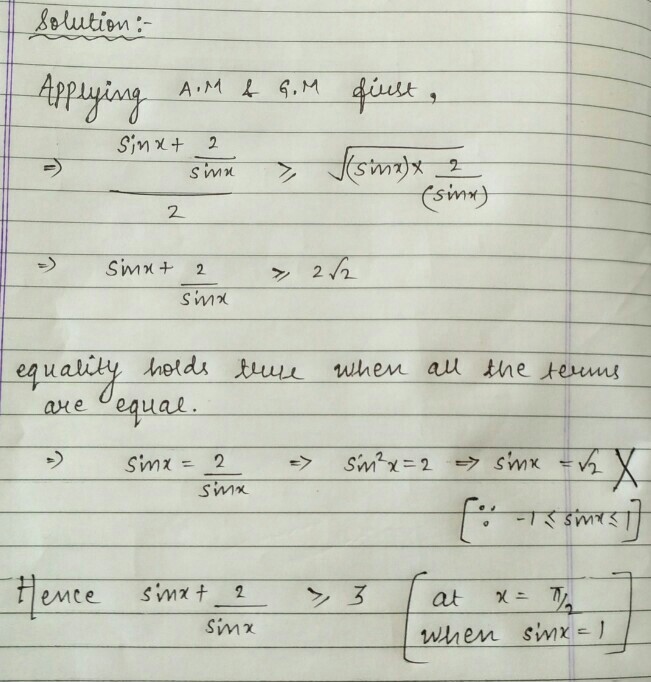
Update: New solution added :)
Solution 1: Let f ( θ ) = sin θ + sin θ 2 Then for minimization, we must have f ′ ( θ ) = cos θ − sin 2 θ 2 ⋅ cos θ = cos θ ( 1 − sin 2 θ 2 ) = 0 Then, under the domain ( 0 , π ) ,
Case 1 cos θ = 0 ⟹ θ = 2 π Case 2 (not possible) 1 − sin 2 θ 2 = 0 ⟹ sin 2 θ = 2 ≥ 1
As θ → 0 + and θ → π − , the value of f approaches + ∞ . Hence, the minimum value occurs at θ = 2 π , and f ( 2 π ) = sin 2 π + sin 2 π 2 = 3
Solution 2: @Raj Rajput @Calvin Lin I think Titu's lemma also works for this problem, since θ ∈ ( 0 , π ) , and thus sin θ > 0 . We have sin θ + sin θ 2 = 1 sin θ + sin θ 1 + sin θ 1 ⩾ 1 + sin θ ( sin θ + 1 ) 2 + sin θ 1 = sin θ + 1 + sin θ 1 Equality occurs when sin θ + sin θ 2 = sin θ + 1 + sin θ 1 ⟹ sin θ 1 = 1 ⟹ sin θ = 1 ⟹ θ = 2 π Therefore, the minimum value is sin 2 π + sin 2 π 2 = 3 .