AM-GM?

By Cauchy-Schwarz inequality , we have:

$\begin{aligned} \frac {\color{#3D99F6} \sqrt a + \sqrt b}{\sqrt s} & \le \frac {\color{#3D99F6}\sqrt{(1+1)(a+b)}}{\sqrt s} = \frac {\sqrt{2s}}{\sqrt s} = \sqrt 2 \end{aligned}$

Therefore, $c=\boxed 2$ .

Here's a somewhat inelegant solution.

Without loss of generality, we can set $s=1$ (this just scales $a$ and $b$ by the same factor and doesn't affect the final result). So we have $b=1-a$ , and we want to maximise $f(a)=\sqrt{a}+\sqrt{1-a}$ , where $0 \le a \le 1$ .

We can use calculus for this, but it's neater to observe that both $\sqrt{a}$ and $\sqrt{1-a}$ are concave functions, so their sum is, too. Also, $f(a)$ is symmetric about $a=\frac12$ ; these two facts mean its maximum value can only occur at $a=0$ (and $a=1$ ), or at $a=\frac12$ . It's easy to check that the largest of these is when $a=\frac12$ , giving $c=2$ .

Alternatively, if we say $a=x^2$ and $b=y^2$ , this problem becomes "maximise $x+y$ subject to $x^2+y^2=1$ ", which is a slightly more familiar formulation and can be solved in a number of different ways (for instance, geometrically - plotting in the $x-y$ plane, the constraint is a circle and the function to be maximised a straight line).

We know that $\frac{\sqrt{a}+\sqrt{b}}{\sqrt{s}}\le \sqrt{c}$ . Squaring both sides of the equation (they are both positive) we get $\frac{a+b+2\sqrt{ab}}{s}\le c$ . From AM-GM (geometric mean is always less or equal the arithmetic one) we know that $\sqrt{ab}\le \frac{a+b}{2}$ which means $2\sqrt{ab}\le a+b=s$ . Therefore $\frac{a+b+2\sqrt{ab}}{s}\le \frac{a+b+s}{s}=\frac{2s}{s}=2 \le c$ , so $c=\boxed{2}$ (because $c$ is the maximum and this expression cannot be greater than 2).

this problem is equivalent to minimizing $\dfrac{a+b}{r}$ for the eqn $a^2+b^2=r^2$ .

Geometrically, this is the equivalent of finding the line tangent to a circle with the eqn $a+b= k$ , i.e a $45^\circ$ line.

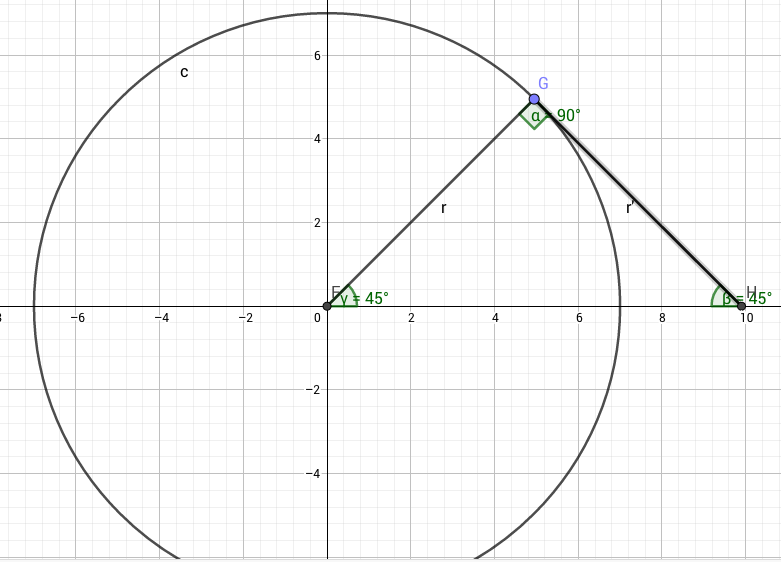
this is an isosceles right triangle, meaning we would have $\dfrac{\sqrt{r^2+r^2}}{r}$ be the minimum, i.e $\boxed{\sqrt{2}}$

Hint :

Use the power mean inequality, i.e.

$\sqrt[p]{\frac{a_1^p+a_2^p+...\ +\ a_n^p}{n}}\ge\sqrt[q]{\frac{a_1^q+a_2^q+...\ +\ a_n^q}{n}}$

where, $\displaystyle a_i$ is a positive real number and $\displaystyle p>q$

Substitute $x = \sqrt{a}$ and $y = \sqrt{b}$ to the original expression yielding $\dfrac{x + y}{\sqrt{x^2 + y^2}}$ .

Now by the QM-AM inequality $\dfrac{x + y}{\sqrt{x^2 + y^2}} = \dfrac{x + y}{2} \sqrt{\dfrac{2}{x^2 + y^2}} \sqrt{2} \leq \sqrt{\dfrac{x^2 + y^2}{2}} \sqrt{\dfrac{2}{x^2 + y^2}}\sqrt{2} = \sqrt{2},$

where equality is attained when $x = y$ .

Hence $c = \boxed{2}$ .

a = u²

b = v²

s = a + b = u² + v² = r²

u = r cos(t)

v = r sin(t)

y = cos(t) + sin(t)

y' = -sin(t) + cos(t) = 0

t = pi/4 en y = sqrt(2)