A.M - G.M equality. :D
Algebra
Level
3
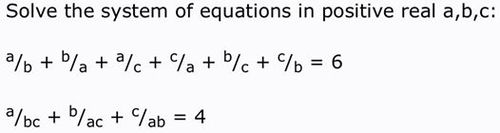 Solve for a,b,c . :D
Solve for a,b,c . :D
a=b = 4/3 . c=3/4
a=b=c= 3/4
a=c = 3/4 , c = 4/3
a=b=c= 4/3
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
From AM-GM inequality, we have b a + a b ≥ 2 and analogously c b + b c ≥ 2 , a c + c a ≥ 2 . Summing up these inequalities nets us: b a + a b + c b + b c + a c + c a ≥ 6 , which has equality only at b a = a b , c b = b c , a c = c a or equivalently a 2 = b 2 = c 2 , further simplifying to a = b = c since we have a , b , c ∈ R + . SInce our given conditions have this equality, this means we indeed have a = b = c for these set of equations.
Substituting a = b = c into the second equation nets us 3 ∗ a 2 a = a 3 = 4 and consequently a = b = c = 4 3