Amazing Circle.
Geometry
Level
3
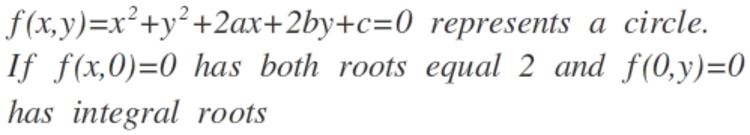 Find the sum of possible positive values of b. [ Both the roots of f(x,0) are equal and have value 2 ]
Find the sum of possible positive values of b. [ Both the roots of f(x,0) are equal and have value 2 ]
The answer is 4.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If f ( x , 0 ) = 0 has both roots equal to x = 2 , then x 2 + 2 a x + c = ( x − 2 ) 2 = x 2 − 4 x + 4 = 0 ⇒ a = − 2 , c = 4 . If f ( 0 , y ) = 0 has only integral roots, then y 2 + 2 b y + 4 = 0 , or:
y = 2 − 2 b ± 4 b 2 − 1 6 = − b ± b 2 − 4 (i).
We require the discriminant in (i) to be a perfect square if y ∈ Z . Thus, b 2 − 4 = N 2 ⇒ b 2 − N 2 = ( b + N ) ( b − N ) = 4 . The positive divisors of 4 are just 1, 2, or 4, which testing in each factor gives:
b + N = 2 , b − N = 2 ⇒ b = 2 (ii)
b + N = 4 , b − N = 1 ⇒ b = 2 5 (iii).
Substituting (ii) and (iii) back into (i) yields:
b = 2 ⇒ y = − 2 ± 4 − 4 = − 2
b = 2 5 ⇒ y = − 2 5 ± 4 2 5 − 4 = − 2 5 ± 2 3 = − 1 , − 4 .
So the sum of all positive b equals 2 + 2 5 = 4 . 5 .