Amazingly alluring result

Here's a complex numbers approach. Let the vertex of the triangle be 1, w, v. Where v = w^2. Since these are cube roots of unity, we have 1 + w + v = 0, wv = 1. Let P(z) be a compex number on a circle of unit radius and center as origin. Now, PA^2 + PB^2 + PC^2 = |z - 1|^2 + |z - w|^2 + |z - v|^2 If we write conjugate of z as c for a while and use|z|^2 = zc, we get the following expression. = (z -1)(c -1) + (z - w)(c - v) + (z - v)(c - w) = 3zc + 3 - z - c - zv - cw - zw - cv = 3 + 3 - (1 + w + v)(z + c) = 6 - 0(z + c) = 6.

It's sufficient to take into consideration one of the vertex of the triangle (which is, in fact, one of the point of the circumcircle). WLOG, let's consider that point P is at vertex A. So the distance PA=0. The distances PB and PC are both equal to the length of the side of the equilateral triangle. From sinus theorem we know that: R= l/sin(A) So we substitute R=1 and A=60 (because the triangle is equilateral). We find that the side is sqrt(3). So the answer is 3+3+0=6

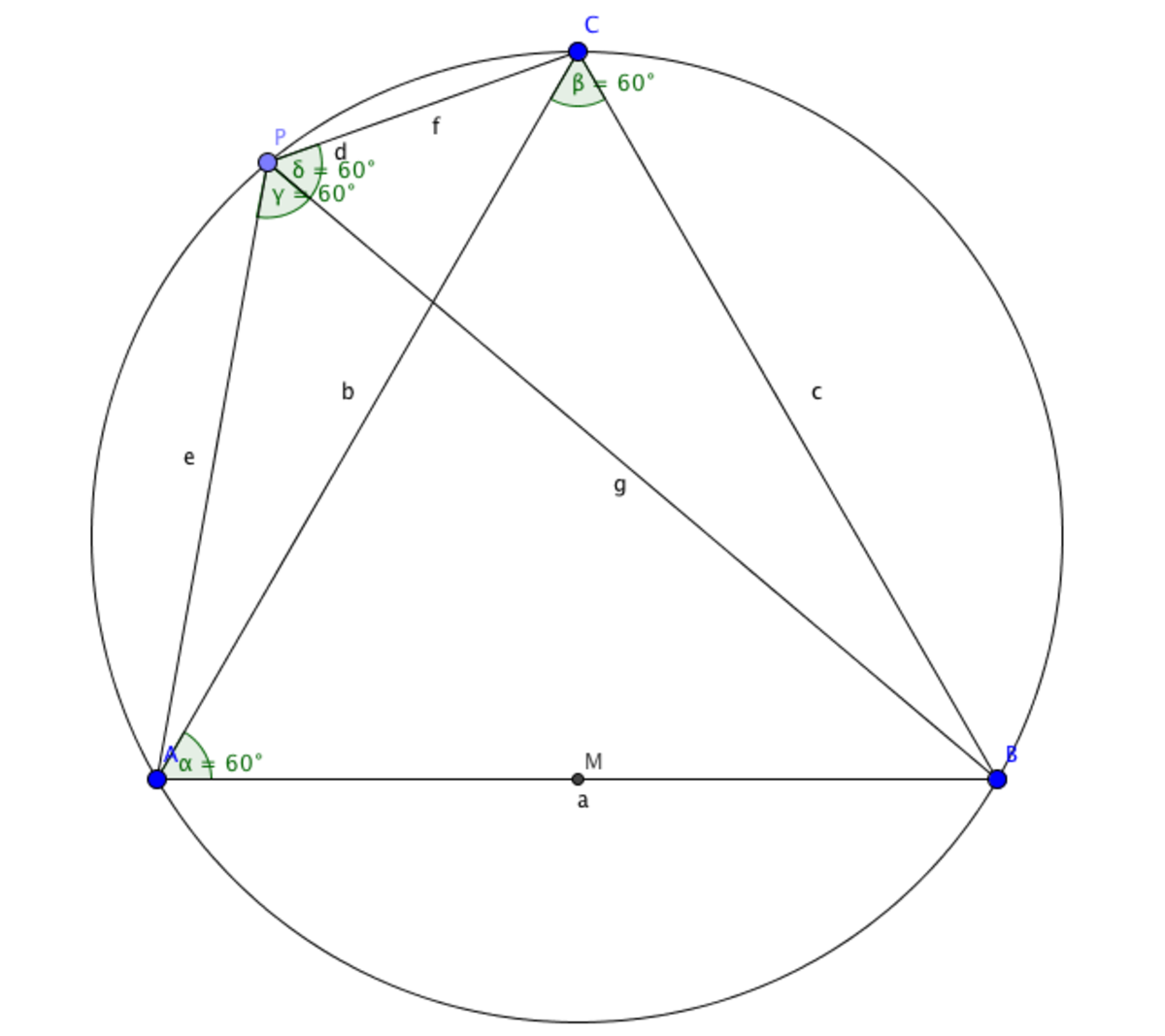
Have the equilateral triangle $ABC$ . Suppose that $P$ is a whatever point in the circumcircle $\omega$ . Now have the cyclic quadrilateral $ABCP$ and her diagonals $AC$ and $PB$ . By the properties of cyclic quadrilaterals can determine that $\angle APB = BPC =CAB = 60^{\circ}$ , $\angle PAC = PBC$ and $\angle PCA = PBA$ .

We know that segment $AB =BC$ then for law of sinus can say that $\dfrac {AB}{sin 60} = \dfrac {PA}{sin PBA} = \dfrac {PB}{sin 60 + PAC}$ and $\dfrac {BC}{sin 60} = \dfrac {PB}{sin 60 + PCA} = \dfrac {PC}{sin PBC}$ as $AB = BC$ then $\dfrac {PB}{sin 60 + PAC}$ $= \dfrac {PB}{sin 60 + PCA}$ and it can be if only if $\angle PAC = \angle PCA$ therefore $PA = PC$ and the height of $ABC$ is $\dfrac { \sqrt 3}{2}$ then $PA = PC = 1$ .

Now the $\triangle APC$ is isosceles and it represent that the segment $PB$ is the diameter of circle $\omega$ therefore $PB = 2$ . By last $PA^{2} + PB^{2} + PC^{2} = 1^{2} + 2^{2} + 1^{2} = 1 + 4 + 1 = 6$

Let the circumcircle be the unit circle $x^2+y^2=1$ and the vertices of the equilateral triangle be $A(0,1); B(-\sqrt{3}/2,-1/2); (\sqrt{3}/2,-1/2)$ . If $P(k, \sqrt{1-k^2})$ be an arbitrary point on the circumcircle, then:

$PA^{2}+PB^{2}+PC^{2} = (k-0)^2 + (\sqrt{1-k^2}-1)^2 + (k + \sqrt{3}/2)^2 + (\sqrt{1-k^2}+1/2)^2 + (k-\sqrt{3}/2)^2 + (\sqrt{1-k^2}+1/2)^2;$

or $k^2 + (1-k^2 -2\sqrt{1-k^2} + 1) + (k^2 + \sqrt{3}k + 3/4) + (1-k^2 + \sqrt{1-k^2} + 1/4) + (k^2 - \sqrt{3}k + 3/4) + (1-k^2 + \sqrt{1-k^2} + 1/4)$ ;

or $(2+2+2) + (\sqrt{3}k - \sqrt{3}k) + (2\sqrt{1-k^2}-2\sqrt{1-k^2});$

or $\boxed{6}.$