Ambiguous Time

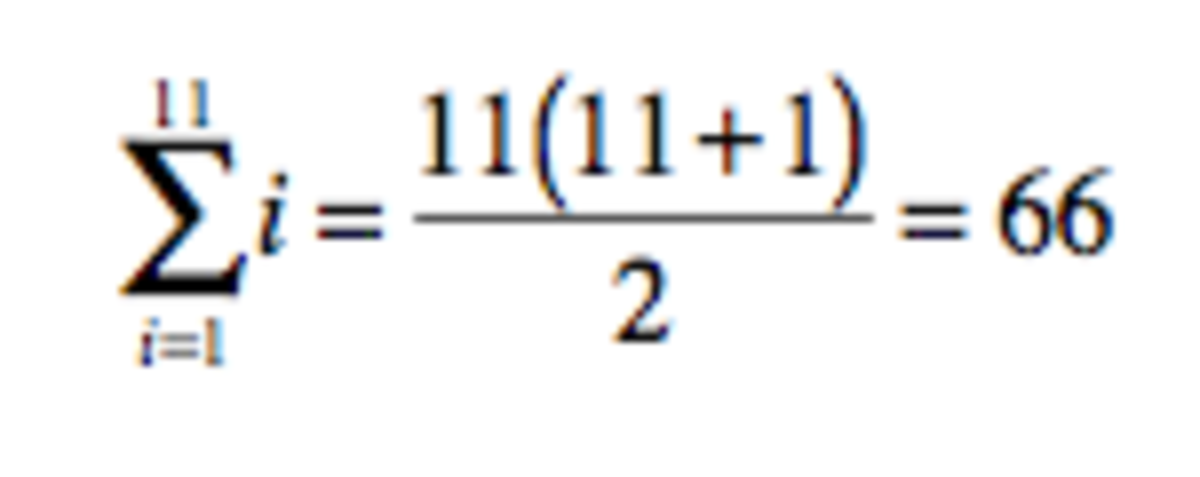
If the hour hand makes a clockwise angle of $h^\circ$ with $12$ o'clock, and the minute hand makes a clockwise angle of $m^\circ$ with $12$ o'clock, then $0 \le h,m < 360$ , and a valid time is shown when $\frac{h}{30} \; = \; H + \frac{m}{360}$ where $H$ is an integer between $0$ and $11$ inclusive (the time is somewhere between $H$ o'clock and $H+1$ o'clock). Note that $H = \big\lfloor \tfrac{h}{30}\big\rfloor$ , and that $m$ is fully determined by $h$ . We want to know the number of values $0 \le h < 360$ which give rise to ambiguous time pairs $(h,m)$ .

A time pair $(h,m)$ may be ambiguous if the pair $(m,h)$ is also a valid time pair. Thus $(h,m)$ is a valid, but ambiguous, time pair if there exist integers $0 \le H,M \le 11$ such that $12h - m \; = \; 360H \hspace{2cm} 12m - h \; =\; 360M$ and hence $h \; = \; \tfrac{360}{143}(12H + M) \hspace{2cm} m \; =\; \tfrac{360}{143}(12M + H)$ If $H,M,H_1,M_1$ are integers between $0$ and $11$ with $12H + M = 12H_1 + M_1$ , then $12(H-H_1) = M_1 - M$ , and so $12$ divides $M_1-M$ . Since $-11 \le M_1 - M \le 11$ , we deduce that $M = M_1$ , and hence $H = H_1$ .

Thus there is an hour angle $h$ with a corresponding minute angle that represents a valid, but possibly ambiguous, time when $h$ is of the form $h \; = \; \tfrac{360}{143}(12H + M) \hspace{2cm} H,M \in \{0,1,2,...,11\}$ and distinct pairs of integers $H,M$ give distinct values of $h$ .

However, this time will not be ambiguous if $H=M$ , since then the same time is being indicated in both positions. Thus there are truly ambiguous times precisely when $H \neq M$ . This means that there are $11 \times 12 = 132$ times in a $12$ -hour period when the time is ambiguous. This means that there are $\boxed{66}$ hand positions in a $12$ -hour period which are ambiguous (with each position of the hands indicating two possible times).

Visually we eventually can see that, for example, a bit past 1:20 is an ambiguous time, since it could also be around 4:06:

Let's define H1 as any time in which the hour is 1, that is 1:10, 1:13, 1:30, and so on are all H1 times. Thus H4 is any time in which the hour is 4. We note that in the image above this is the ONLY ambiguous time combo for H1 and H4.

After some careful thought, we see that a given hour has exactly ONE ambiguous time with each other hour. Thus H1 has 11 ambi-times, one with H0, H2, H3, H4, H5, H6, H7, H8, H9, H10, and H11. H4 will also have 11 ambiguous times, but one of those is with H1...

This gives us the answer as 11 + 10 + 9 + ... + 2 + 1 = 66 ambi-pairs per 12 hours. We can write this as a summation, if we desire:

Finally, it is hopefully clear at this point that an hour CANNOT have an ambi-time with itself, i.e. H1 with H1, although this time would satisfy equations used to find the exact value of an ambi-time (try this!), it would visually look like image below, which is NOT an ambiguous time, since it can only represent one time.