Ampere's Law Exercise (Part 2)
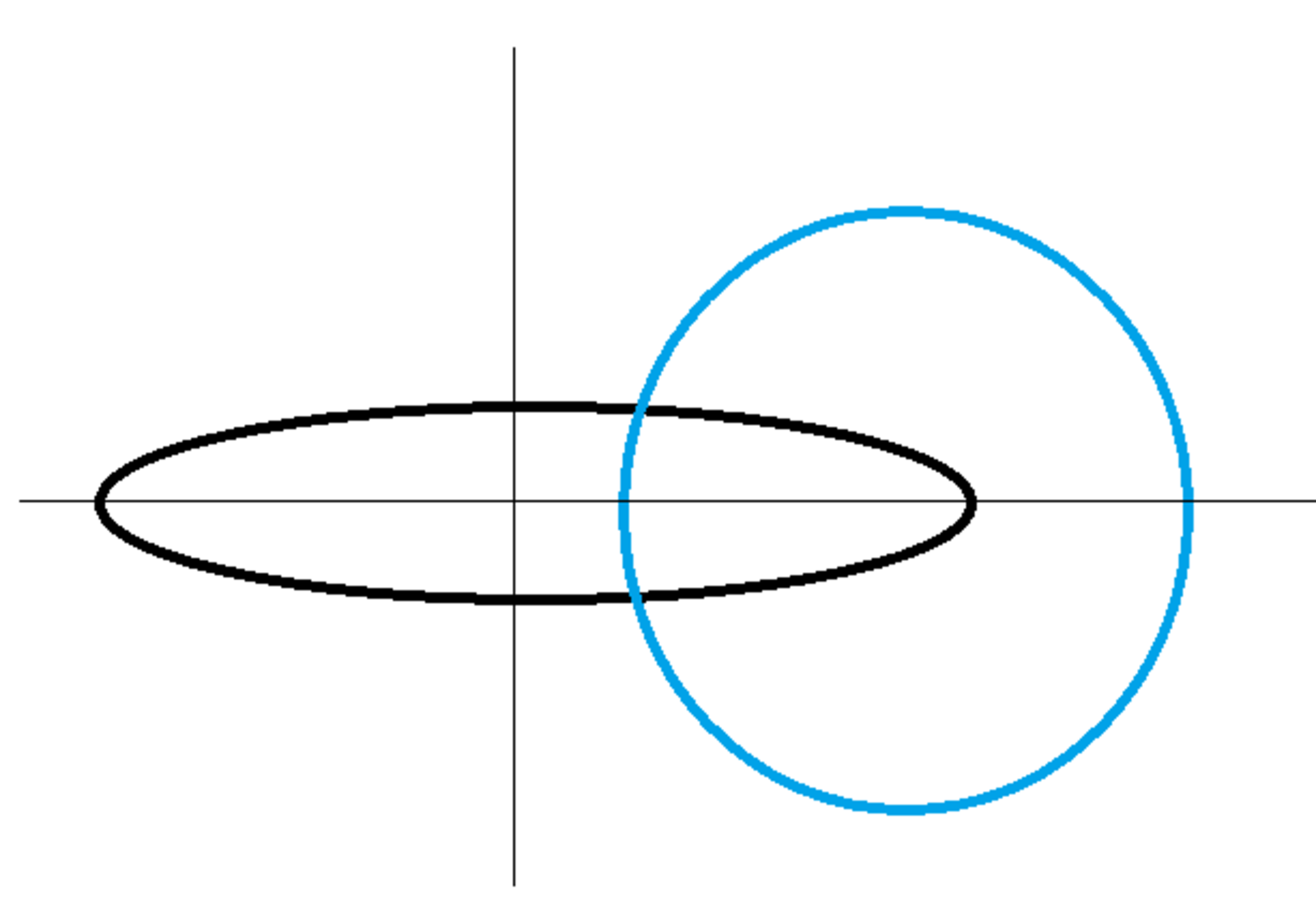
A circular wire loop of radius lies in the plane and has its center at the origin. The loop carries unit of electric current. Consider an integration path consisting of a circle of radius in the plane with its center at . Define the following magnetic line integrals over the "left" and "right" halves of the integration path:
In the above integrals, is the vector magnetic flux density produced by the loop at a particular point. Determine the following ratio:
Details and Assumptions:
1)
Magnetic permeability
2)
You know ahead of time what the denominator of the ratio is
3)
Use the same circulation (clockwise or counter-clockwise) when evaluating both integrals
The answer is 0.179.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider a point on the black circle:
r C 1 = cos θ i ^ + sin θ j ^
An arc length element of this circle is:
d r C 1 = ( − sin θ i ^ + cos θ j ^ ) d θ
Consider a point on the blue circle circle:
r C 2 = cos ϕ i ^ + sin ϕ j ^
An arc length element of this circle is:
d r C 2 = ( − sin ϕ i ^ + cos ϕ j ^ ) d ϕ
Let:
r = r C 2 − r C 1
Now, the magnetic field at a point on the blue circle due to an element of the black circle is:
d B = 4 π μ o I ( ∣ r ∣ 3 d r C 1 × r )
The elementary dot product of this magnetic field along an arc length element of the blue circle is:
d Q = d B ⋅ d r C 2
Now, it is just a matter of substituting expressions and simplifying a bit, to obtain:
d Q = 4 π − 1 ( ( 2 cos ( ϕ ) − 2 cos ( θ ) − 2 cos ( ϕ ) cos ( θ ) + 3 ) 3 / 2 cos ( θ ) − cos ( ϕ ) + cos ( ϕ ) cos ( θ ) ) d θ d ϕ ⟹ d Q = f ( θ , ϕ ) d θ d ϕ
Now, the following quantities:
Q R = ∫ − π / 2 π / 2 ∫ 0 2 π f ( θ , ϕ ) d θ d ϕ
Q L = ∫ π / 2 3 π / 2 ∫ 0 2 π f ( θ , ϕ ) d θ d ϕ
From Ampere's Law: Q L + Q R = 1 and therefore the answer is:
Q R ≈ 0 . 1 7 8 7