A Grid of Pieces

Dan and Sam play a game on a grid, on which each one chooses and puts, in his turn, a single piece like these:

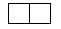
The pieces must not overlap and can't be partially outside of the grid.
The game finishes when someone can't put a piece on the board in his turn following the rules (who is the loser). If Dan begins, who will win? This means, who has a winning strategy?
This is the eleventh problem of the set Winning Strategies .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Not a solution, but a comment. This game is known as Cram , and as far as I know, the general odd-by-odd case is unsolved (but the even-by-even and even-by-odd cases are easy to analyze). If someone has a proof for the 9 × 9 case, I would like to see it.