An absolute value problem

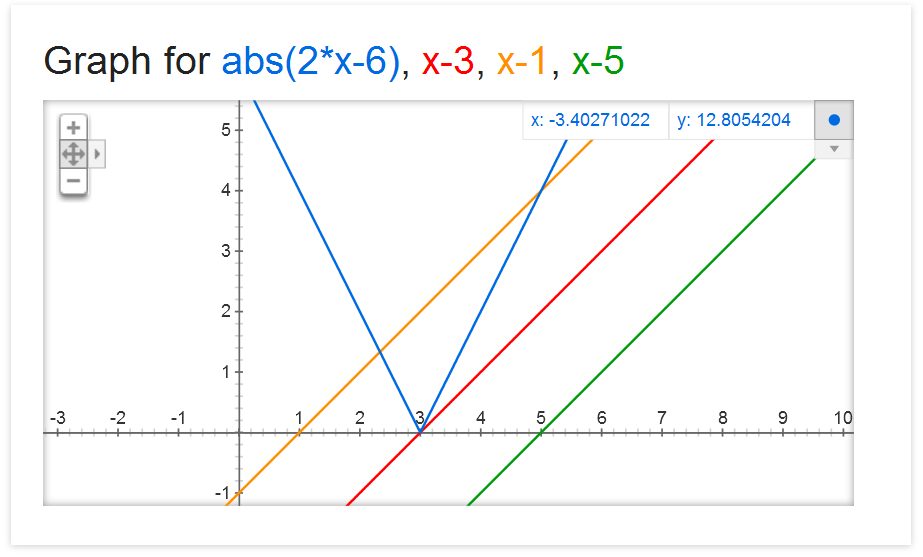
One can easily get the answer by visualizing the graph. However, here is the mathematical solution:

From the properties of absolute value we know that,

• If $|f(x)|>0$ , it'll have $2$ distinct roots.

• If $|f(x)|=0$ , it'll have only $1$ root.

• As, $|f(x)|<0$ is undefined, it won't have any roots.

From the 2nd property, $|2x-6|=0$ will have $1$ root. Let's find the root : $|2x-6|=0$ $\Rightarrow 2|x-3|=0$ $\Rightarrow |x-3|=0$ $\Rightarrow x=3$ As, $|2x-6|=x+k$ , to have $1$ root: $x+k=0$ $\Rightarrow 3+k=0$ $\Rightarrow k=-3$

As, $|2x-6|=x+k$ ; if $k$ increases, $|2x-6|$ will also increase. Thus, from property $1$ , to have $2$ roots the condition will be, $\color{#0C6AC7}{\boxed {k>-3}}$