An algebra problem by A Former Brilliant Member
2 2 x 2 − 1 0 x + 3 + 6 x 2 − 5 x + 1 ≥ 3 2 x 2 − 1 0 x + 3
The set of values of x for which above inequality holds is given by:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
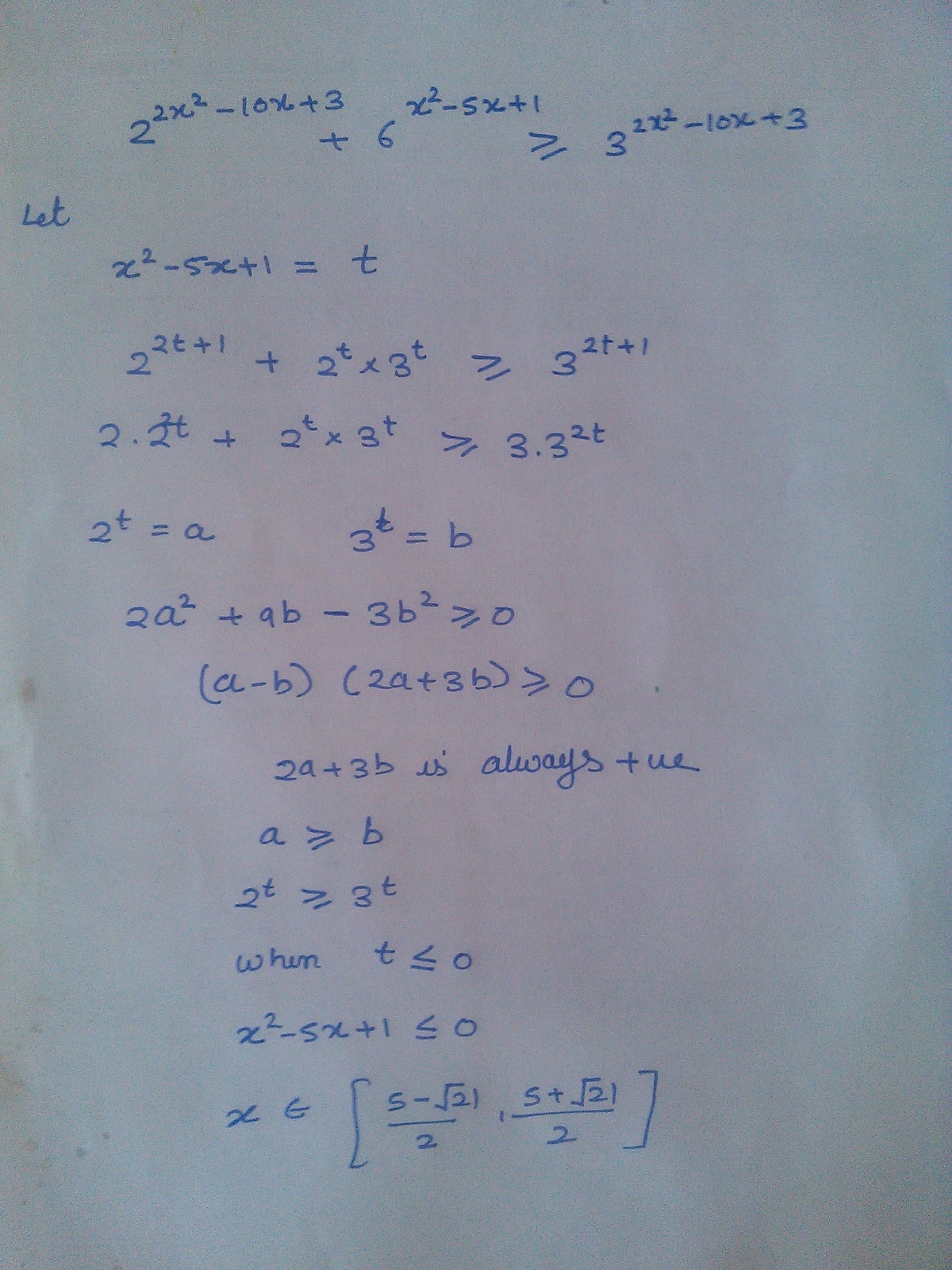
Good solution
X^2 -5X + 1 =T.
SO THE EXPRESSION BECOMES
2^(2T+1) + 6^T >3^(2T+1)
WHEN U FACTORIZEIT BECOMES
{(2^(2T+1)+3^(2T+1))(2^T-3^T)}>0
first EXPRESSION is always greater than zero.when u solve the second expression u get the solution.(use logs)
quickly , thats my soultion x>=- 2.5 log 3, i will try again iam newly in math
Factorization is WRONG although the conclusion is correct!
X^2-5x+1 =a and solve it by using log then we get an equality and solve it